Conservation of Momentum:  Momentum Theorem

In Newtonian mechanics, the conservation of momentum is defined by Newton’s second law of motion.

Newton’s Second Law of Motion

• The rate of change of momentum of a body is proportional to the impressed action and takes place in the direction of the impressed action.
• If a force acts on the body ,linear momentum is implied.
• If a torque (moment) acts on the body,angular momentum is implied.

Reynolds Transport Theorem

A study of fluid flow by the Eulerian approach requires a mathematical modeling for a control volume either in differential or in integral form. Therefore the physical statements of the principle of conservation of mass, momentum and energy with reference to a control volume become necessary.

 This is done by invoking a theorem known as the Reynolds transport theorem which relates the control volume concept with that of a control mass system in terms of a general property of the system.

Statement of  Reynolds Transport Theorem

The theorem states that "the time rate of increase of property N within a control mass system is equal to the time rate of increase of property N within the control volume plus the net rate of efflux of the property N across the control surface”.

Equation of  Reynolds Transport Theorem

After deriving  Reynolds Transport Theorem according to the above statement we get

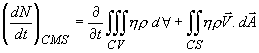(10.9)

In this equation

N - flow property which is transported

η - intensive value of the flow property