|
Application of the Reynolds Transport Theorem to Conservation
of Mass and Momentum
Conservation
of mass The constancy of mass
is inherent in the definition of a control mass system and
therefore we can write
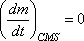 |
(10.13a) |
To develop the analytical
statement for the conservation of mass of a control volume,
the Eq. (10.11) is used with N = m (mass) and η = 1 along
with the Eq. (10.13a).
This gives
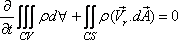 |
(10.13b) |
The Eq. (10.13b) is identical
to Eq. (10.6) which is the integral form of the continuity
equation derived in earlier section. At steady state, the first term on the left hand side of Eq. (10.13b) is
zero. Hence, it becomes
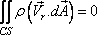 |
(10.13c) |
Conservation of
Momentum or Momentum Theorem The principle of conservation
of momentum as applied to a control volume is usually referred
to as the momentum theorem.
Linear momentum
The first step in deriving the analytical
statement of linear momentum theorem is to write the Eq. (10.11)
for the property N as the linear - momentum
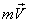 and accordingly η as the velocity
and accordingly η as the velocity
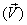 .
Then it becomes .
Then it becomes
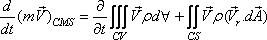 |
(10.14) |
The velocity
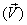 defining the linear momentum in Eq. (10.14) is described
in an inertial frame of reference. Therefore we can substitute
the left hand side of Eq. (10.14) by the external forces
defining the linear momentum in Eq. (10.14) is described
in an inertial frame of reference. Therefore we can substitute
the left hand side of Eq. (10.14) by the external forces
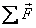 on the control mass system or on the coinciding control volume
by the direct application of Newton’s law of motion.
This gives on the control mass system or on the coinciding control volume
by the direct application of Newton’s law of motion.
This gives
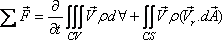 |
(10.15) |
This Equation is the
analytical statement of linear momentum theorem.
In the analysis of finite
control volumes pertaining to practical problems, it is convenient
to describe all fluid velocities in a frame of coordinates
attached to the control volume. Therefore, an equivalent form
of Eq.(10.14) can be obtained, under the situation, by substituting
N as and accordingly η as 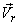 , we get , we get
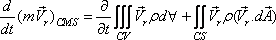 |
(10.16) |
With the help of the Eq. (10.12)
the left hand side of Eq. can be written as
where
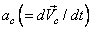 is the rectilinear acceleration of the control volume (observed
in a fixed coordinate system) which may or may not be
a function of time. From Newton’s law of motion is the rectilinear acceleration of the control volume (observed
in a fixed coordinate system) which may or may not be
a function of time. From Newton’s law of motion
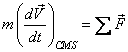 |
|
Therefore, 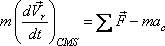 |
(10.17) |
The Eq. (10.16) can be written in consideration
of Eq. (10.17) as
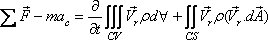 |
(10.18a) |
At steady state, it becomes
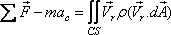 |
(10.18b) |
In case of an inertial control
volume (which is either fixed or moving with a constant rectilinear
velocity),
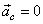 and hence Eqs (10.18a) and (10.18b) becomes respectively
and hence Eqs (10.18a) and (10.18b) becomes respectively
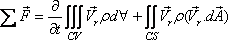 |
(10.18c) |
and 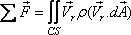 |
(10.18d) |
The Eqs (10.18c) and (10.18d)
are the useful forms of the linear momentum theorem as applied
to an inertial control volume at unsteady and steady state
respectively, while the Eqs (10.18a) and (10.18b) are the
same for a non-inertial control volume having an arbitrary
rectilinear acceleration.
In general, the external forces
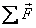 in Eqs (10.14, 10.18a to 10.18c) have two components - the
body force and the surface force. Therefore we can write
in Eqs (10.14, 10.18a to 10.18c) have two components - the
body force and the surface force. Therefore we can write
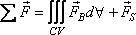 |
(10.18e) |
where 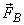 is the body force per unit volume and is the body force per unit volume and 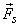 is the area weighted surface force. is the area weighted surface force.
Angular
Momentum
The angular momentum or moment of momentum
theorem is also derived from Eq.(10.10) in consideration of
the property N as the angular momentum and accordingly η as the angular momentum per unit mass. Thus,
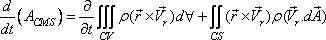 |
(10.19) |
where AControl mass system
is the angular momentum of the control mass system. . It has to be noted that the origin for the angular
momentum is the origin of the position vector
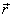
The term on the left hand side of Eq.(10.19) is the time rate
of change of angular momentum of a control mass system, while
the first and second terms on the right hand side of the equation
are the time rate of increase of angular momentum within a
control volume and rate of net efflux of angular momentum
across the control surface.
The velocity 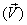 defining
the angular momentum in Eq.(10.19) is described in an inertial
frame of reference.Therefore, the term defining
the angular momentum in Eq.(10.19) is described in an inertial
frame of reference.Therefore, the term
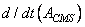 can be substituted by the net moment ΣM applied to the
system or to the coinciding control volume. Hence one can
write Eq. (10.19) as can be substituted by the net moment ΣM applied to the
system or to the coinciding control volume. Hence one can
write Eq. (10.19) as
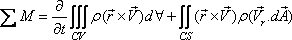 |
(10.20a) |
At steady state
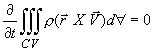 |
|
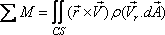 |
(10.20b) |
End of Lecture 10!
To start next lecture click next button or select from left-hand-side.
|
|