|
Derivation of Reynolds
Transport Theorem
To formulate the relation between
the equations applied to a control mass system and those applied
to a control volume, a general flow situation is considered
in Fig. 10.3 where the velocity of a fluid is given relative
to coordinate axes ox, oy, oz. At any time t, a control
mass system consisting of a certain mass of fluid is
considered to have the dotted-line boundaries as indicated.
A control volume (stationary relative to the coordinate axes)
is considered that exactly coincides with the control mass
system at time t (Fig. 10.3a). At time t+δt, the control
mass system has moved somewhat, since each particle constituting
the control mass system moves with the velocity associated
with its location.
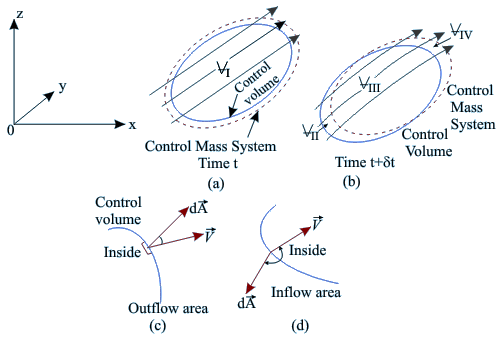
Fig 10.3 Relationship
between Control Mass system and control volume concepts in the analysis
of a flow field
Consider, N to be the total
amount of some property (mass, momentum, energy) within the
control mass system at time t, and let η be the amount
of this property per unit mass throughout the fluid. The time
rate of increase in N for the control mass system is now formulated
in terms of the change in N for the control volume. Let the
volume of the control mass system and that of the control
volume be  1at time t with both of them coinciding
with each other (Fig. 10.3a). At time t + δt, the volume
of the control mass system changes and comprises volumes 1at time t with both of them coinciding
with each other (Fig. 10.3a). At time t + δt, the volume
of the control mass system changes and comprises volumes  III
and III
and 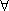 IV(Fig. 10.3b). Volumes IV(Fig. 10.3b). Volumes  II and II and  IV are the intercepted regions between the control
mass system and control volume at time t+δt. The increase
in property N of the control mass system in time δt
is given by IV are the intercepted regions between the control
mass system and control volume at time t+δt. The increase
in property N of the control mass system in time δt
is given by
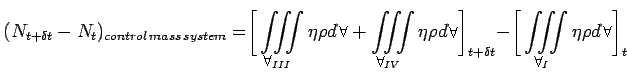
where,d represents an element
of volume. After adding and subtracting represents an element
of volume. After adding and subtracting
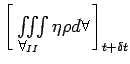 to the right hand side of the equation and then dividing throughout
by δt, we have to the right hand side of the equation and then dividing throughout
by δt, we have 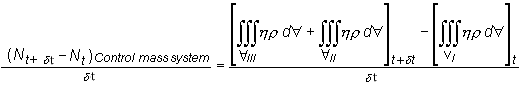
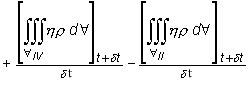 (10.9)
(10.9)
The left hand side of Eq.(10.9)
is the average time rate of increase in N within the control
mass system during the time δt.
In the limit as δt approaches zero, it becomes dN/dt
(the rate of change of N within the control mass system at
time t ).
In the first term of the right hand side of the above equation
the first two integrals are the amount of N in the control
volume at time t+δt, while the third integral is the
amount N in the control volume at time t. In the limit, as
δt approaches zero, this term represents the time rate
of increase of the property N within the control volume and
can be written as
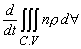
The next term, which is the time rate of flow of N out of
the control volume may be written, in the limit 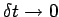 as
as
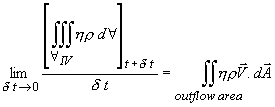 |
|
In which 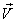 is the velocity vector and is the velocity vector and 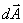 is an elemental area vector on the control surface. The sign
of vector
is an elemental area vector on the control surface. The sign
of vector 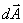 is positive if its direction is outward normal (Fig.
10.3c). Similarly, the last term of the Eq.(10.9) is the rate
of flow of N into the control volume is, in the limit δt
→ 0 is positive if its direction is outward normal (Fig.
10.3c). Similarly, the last term of the Eq.(10.9) is the rate
of flow of N into the control volume is, in the limit δt
→ 0
The minus sign is needed as
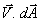 is
negative for inflow. The last two terms of Eq.(10.9)
may be combined into a single one is an integral over the
entire surface of the control volume and is written as is
negative for inflow. The last two terms of Eq.(10.9)
may be combined into a single one is an integral over the
entire surface of the control volume and is written as 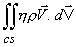 .
This term indicates the net rate of outflow N from the
control lume. Hence, Eq.(10.9) can be written as .
This term indicates the net rate of outflow N from the
control lume. Hence, Eq.(10.9) can be written as
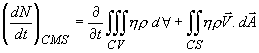 |
(10.10) |
The Eq.(10.10) is known as Reynolds
Transport Theorem
Important Note: In
the derivation of Reynolds transport theorem (Eq. 10.10), the
velocity field was described relative to a reference
frame xyz (Fig. 10.3) in which the control volume was kept
fixed, and no restriction was placed on the motion of the
reference frame xyz. This makes it clear that the fluid
velocity in Eq.(10.10) is measured relative to the control
volume. To emphasize this point, the Eq. (10.10) can be written
as
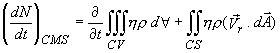 |
(10.11) |
where the fluid velocity
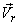 ,
is defined relative to the control volume as ,
is defined relative to the control volume as
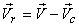 |
(10.12) |
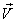 and
and 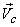 are now the velocities of fluid and the control volume
respectively as observed in a fixed frame of reference.
The velocity are now the velocities of fluid and the control volume
respectively as observed in a fixed frame of reference.
The velocity 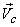 of the control volume may be constant or any arbitrary function
of time. of the control volume may be constant or any arbitrary function
of time.
Back
to the Original Slide
|