Continuity Equation: Integral Form

Let us consider a control volume 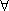  bounded by the control surface S. The efflux of mass across the control surface S is given by

where 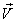is the velocity vector at an elemental area( which is treated as a vector by considering its positive direction along the normal drawn outward from the surface).

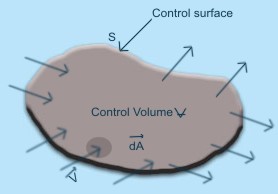
Fig 10.2  A Control Volume for the Derivation of Continuity Equation (integral form)

The rate of mass accumulation within the control volume becomes

where d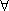 is an elemental volume, ρ is the density and 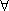is the total volume bounded by the control surface S. Hence, the continuity equation becomes (according to the statement given by Eq. (9.1))

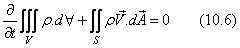(10.6)

The second term of the Eq. (10.6) can be converted into a volume integral by the use of the Gauss divergence theorem as

Since the volume 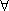does not change with time, the sequence of differentiation and integration in the first term of Eq.(10.6) can be interchanged.
Therefore Eq. (10.6) can be written as

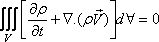(10.7)

Equation (10.7) is valid for any arbitrary control volume irrespective of its shape and size. So we can write

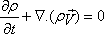(10.8)