Stream Function in Three Dimensional and Compressible Flow
Stream Function
in Three Dimensional Flow
In case of a three dimensional
flow, it is not possible to draw a streamline with a single
stream function.
An axially symmetric
three dimensional flow is similar to the two-dimensional case
in a sense that the flow field is the same in every plane
containing the axis of symmetry.
The equation of continuity
in the cylindrical polar coordinate system for an incompressible
flow is given by the following equation
For an axially symmetric flow
(the axis r = 0 being the axis of symmetry), the term 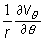 =0 ,and
simplified equation is satisfied by functions defined
as
 |
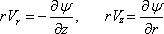(10.4) |
The function ψ , defined by the Eq.(10.4) in case of a three dimensional
flow with an axial symmetry, is called the stokes
stream function.
Stream Function
in Compressible Flow
For compressible flow,
stream function is related to mass flow rate instead of volume
flow rate because of the extra density term in the continuity
equation (unlike incompressible flow)
The continuity equation
for a steady two-dimensional compressible flow is given by
Hence a stream function ψ
is defined which will satisfy the above equation of
continuity as
 |
|
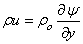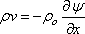 [where ρ0 is a reference density] |
(10.5) |
ρ0
is used to retain the unit of ψ same as that in
the case of an incompressible flow. Physically,
the difference in stream function between any two streamlines
multiplied by the reference density ρ0 will
give the mass flow rate through the passage of unit width
formed by the streamlines.
|
