Physical Significance of Stream Funtion ψ

Figure 10.1 illustrates a two dimensional flow.

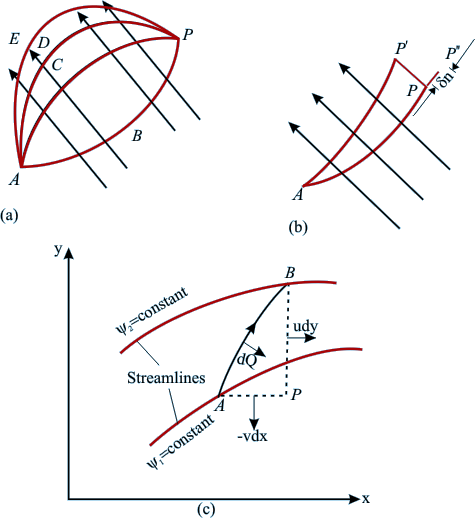
Fig 10.1   Physical Interpretation of Stream Function

Let A be a fixed point, whereas P be any point in the plane of the flow. The points A and P are joined by the arbitrary lines ABP and ACP. For an incompressible steady flow, the volume flow rate across ABP into the space ABPCA (considering a unit width in a direction perpendicular to the plane of the flow) must be equal to that across ACP. A number of different paths connecting A and P (ADP, AEP,...) may be imagined but the volume flow rate across all the paths would be the same. This implies that the rate of flow across any curve between A and P depends only on the end points A and P.

Since A is fixed, the rate of flow across ABP, ACP, ADP, AEP (any path connecting A and P) is a function only of the position P. This function is known as the stream function ψ.

The value of ψ at P represents the volume flow rate across any line joining P to A.
The value of ψ at A is made arbitrarily zero. If a point P’ is considered (Fig. 10.1b),PP’ being along a streamline, then the rate of flow across the curve joining A to P’ must be the same as across AP, since, by the definition of a streamline, there is no flow across PP'

The value of ψ thus remains same at P’ and P. Since P’ was taken as any point on the streamline through P, it follows that ψ is constant along a streamline. Thus the flow may be represented by a series of streamlines at equal increments of ψ.

In fig (10.1c) moving from A to B net flow going past the curve AB is

The stream function, in a polar coordinate system is defined as

The expressions for V_r and V_θ in terms of the stream function automatically satisfy the equation of continuity given by