|
Stream Function
Let us consider a two-dimensional incompressible
flow parallel to the x - y plane in a rectangular cartesian
coordinate system. The flow field in this case
is defined by
u = u(x, y, t)
v = v(x, y, t)
w = 0 |
|
The equation of continuity is
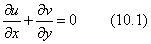 |
(10.1) |
If
a function ψ(x, y, t) is defined in the manner
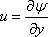 |
(10.2a) |
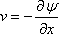 |
(10.2b) |
so that it automatically satisfies the equation
of continuity (Eq. (10.1)), then the function is known as
stream function.
Note that for a steady flow, ψ is a function
of two variables x and y only.
Constancy of ψ on a Streamline
Since ψ is a point function, it
has a value at every point in the flow field.
Thus a change in the stream function ψ can be written
as
The equation of a streamline is given by
It follows that dψ = 0 on a streamline.This
implies the value of ψ is constant along a streamline.
Therefore, the equation of a streamline can be expressed in
terms of stream function as
| ψ(x, y) = constant |
(10.3) |
Once the function ψ is known, streamline
can be drawn by joining the same values of ψ in the flow
field.
Stream
function for an irrotational flow
In case of a two-dimensional irrotational
flow
Conclusion drawn:For an irrotational flow, stream function
satisfies the Laplace’s
equation
|