Problem-4
A cube of 80 mm long edges has its vertical faces equally inclined to the VP. It is cut by an AIP in such a way that the true shape of the cut part is a regular hexagon. Determine the inclination of the cutting plane with the HP. Draw FV, sectional TV and true shape of the section.
Solution:
The solution is shown in figure 10. Draw TV and FV of the cube.  As the true shape of the section is a hexagon, the cutting plane must cut the prism at 6 points. The cutting plane will cut two edges of the top, two edges of the base and two vertical edges. The Points of intersection at two vertical edges will be farthest from each other. These points will represent the two opposite corners of the hexagon and the distance between them will be equal to b( b1)– d( d1).

Draw a line 3–6 = b( b1)– d( d1). Draw a circle with 3–6 as a diameter. Inscribe a hexagon 1– 2–3–4–5–6 in it as shown. Measure the distance between 1–2 and 4–5, i.e., PQ.   In the front view,  locate 3’ at the midpoint of b’( d’)– b1’( d1’). With 3’ as a centre and radius = ½( PQ), cut arcs on a’ b’ and b1’ c1’ to locate 1’ and 4’ respectively. Join 1’–4’ for the required cutting plane. Measure θ.

Draw X1 Y1 parallel to 1’–4’. Redraw hexagon 1–2–3–4–5–6 as 11–21–31–41–51–61 such that pq is parallel to X1 Y1. Project all the corners of the hexagon in FV. 2’, 6’ and 5’ will coincide with 1’, 3’ and 4’ respectively. Project 1’, 2’, 3’, etc., to 1, 2, 3, etc., on the corresponding edges in TV to obtain the section. 3 and 6 will coincide with d( d1) and b( b1) respectively

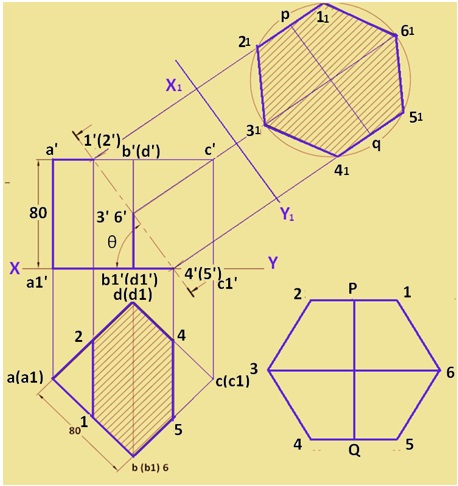
Figure 10. Solution to problem - 4