4. Section plane Inclined to VP

Problem-3 A pentagonal pyramid has its base on the HP. Base of the pyramid is 30 mm in side, axis 50 mm long. The edge of the base nearer to VP is parallel to it. A vertical section plane, inclined at 45° to the VP, cuts the pyramid at a distance of 6 mm from the axis.  Draw the top view, sectional front view and the auxiliary front view on an AVP parallel to the section plane.
Solution:
The solution is shown in figure 9. The Front view and top view of the pyramid is first drawn. The vertical section which is inclined at 45° to VP is shown by the line HT inclined at 45° to XY line. Since the section plane passes through a point 6 mm from the axis of the pyramid, a circle of radius 6 mm is drawn in the top view. The line HT is drawn such that it is tangent to this circle.  The sectional front view of the object is obtained by drawing vertical projectors  and its intersection with the respective  slant edges in the front view. Since point 2 (in the top view) is in the line ob, which is vertical, the projection of point 2’ is obtained in the following manner. With centre O and radius o-2, draw an arc  to intersect the  line o-c at 2₁.  Project point 2₁ in the top view to point 2’ in the Front view. Draw a horizontal projector from 2’ to intersect the line o’-b’ at 2’.  The section front view is shown by the hatched area in the front view.
The auxiliary front view is drawn to obtain the true shape of the section. This is obtained by the auxiliary projection method shown in figure 9 .

 

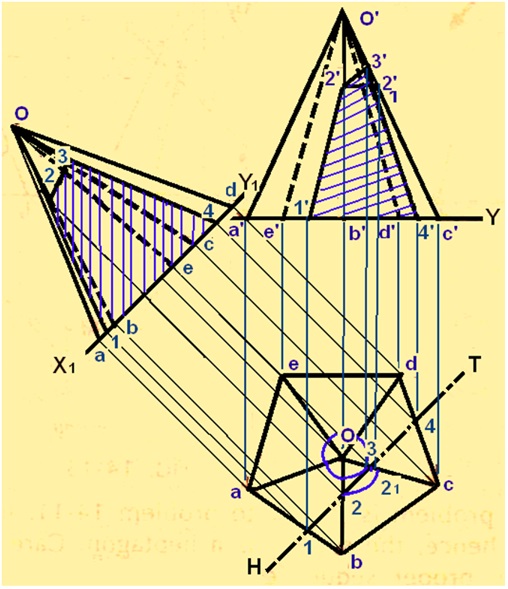
Figure 9. Solution to problem – 3.