2. Section plane parallel to HP

Problem -1: A triangular prism, side of base 30 mm and axis 50 mm long is lying on the HP on one of its rectangular faces with its axis inclined at 30° to the VP. It is cut by a horizontal section plane at a distance of 12 mm above the ground. Draw its front view, side view and sectional top view

Solution: The Top view and front view  of the triangular prism with respect to the projection planes is drawn first. In the Front view, the section plane (line V-T) which is parallel to HP will be a line parallel to and 12 mm above XY line.  It is evident from figure 7. that the line VT intersects with the edges a’-b’ at 1’, a’-c’ at 2’, d’-e’ at 4’  and d’-f’ at 3’.  Draw verticalprojectors from this points to meet the edges a-b at 1, a-c at 2, e-d at 4 and d-f at 3 respectively. When the top portion of the prism is removed, the top view  will beobtained as a rectangle, i.e the hatched region bounded by 1-2-3-4.

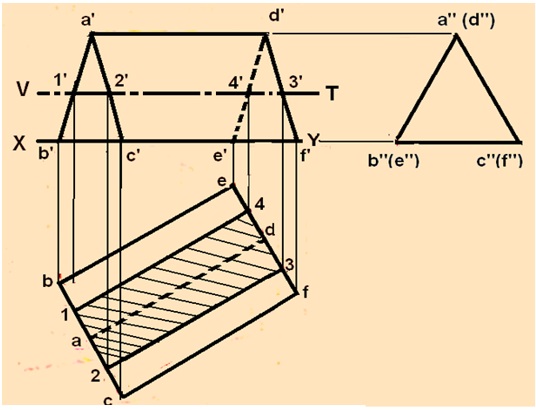
Figure 7. Sectional view of the object in problem-1.

3. Section plane parallel to HP

Problem-2: A pentagonal pyramid, side of base 30 mm and axis 65 mm long, has its base horizontal and an edge of the base parallel to the VP. A horizontal section plane cuts it at a distance of 25 mm above the base. Draw its front view and sectional top view.
Solution : Figure 8 shows the solution of the problem. The  sectional view is obtained in the same manner as in probel-1. Here the intersection the slant edges of the pyramid with the section plane is projected  on to the respective edges in the top view.

 

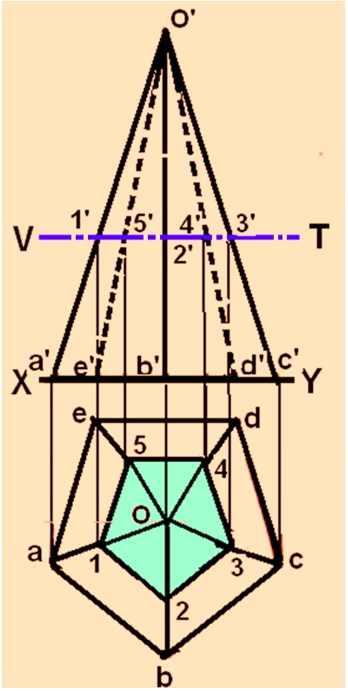
Figure 8. Sectional view for the problem-2.