Conic

Conic is defined as the locus of a point moving in a plane such that the ratio of its distance from a fixed point and a fixed straight line is always constant.

• Fixed point  is called Focus
• Fixed line is called Directrix

This is illustrated in figure 2.

 

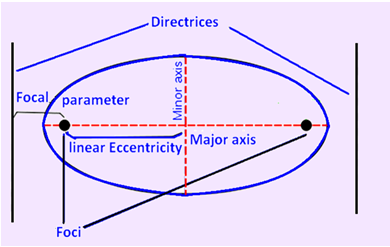
Figure 2.  illustrates the directrices and foci of a conic curve.

 

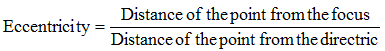
When eccentricity
<  1   Ellipse
=1    Parabola
> 1    Hyperbola     

 eg. when e=1/2, the curve is an  Ellipse, when e=1, it is a parabola and when e=2, it is a hyperbola.  Figure 3 shows the ellipse, parabola and hyperbola.

 

 

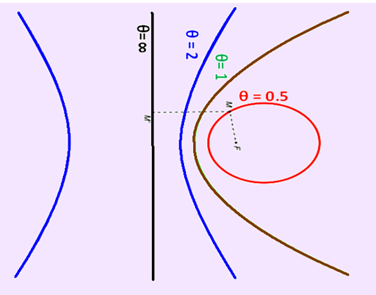
Figure 3 shows the relationship of eccentricity with different conic curves.