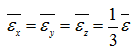Also,

(4.172)

The total energy is thus divided equally in each direction, called a degree of freedom, so that we have equipartition of energy among the three translational degrees of freedom. Molecules may posses other degrees of freedom or modes of storing energy. They have moments of inertia and mass, and hence can have kinetic energy of rotation as well. A molecule can have three rotational degrees of freedom. Since the molecules are not rigid, they also expected to oscillate or vibrate as they collide with other molecules, giving rise to still more degrees of freedom. Study of the storage of energy in molecule shows that if the energy associated with any degree of freedom is a quadratic function of the variable specifying the degree of freedom, the average value of the corresponding energy is equal to . The kinetic energy associated with v_x is a quadratic function of v_x, and the mean value of ε_x, as found earlier, is . For rotation, the kinetic energy is  and the mean rotational kinetic energy associated per degree of freedom is  .Similarly, for a simple harmonic oscillator, the potential energy is , where k is the force constant , and the mean potential energy is . Therefore, for all the degrees of freedom in which energy is a quadratic function, equal amounts of energy are associated, and the total energy of a molecule is shared equally among the degrees of freedom. This underlies the principle of equipartion of energy.