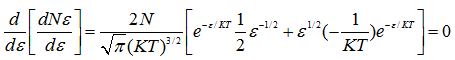Energy Distribution Function

The molecules of gas at a certain temperature have velocities and hence different kinetic energies. The translational kinetic energy ε of a molecule of mass m moving with a velocity v, is

(4.161)

     Differentiating,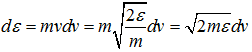
An expression for the molecules with translational kinetic energies within a certain range, say between ε and ε + dε will now be derived. From Maxwell-Boltzmann distribution function, we get,

(4.162)

Therefore,

(4.163)

The notation of dN_v has been changed to dN_ε, since the distribution is now expressed in terms of ε. The above equation is known as the Maxwell-Boltzmann energy distribution function where dN_ε represents the number of molecules having energy between ε and ε + dε. Figure 4.22 shows the distribution of energy of molecules. The most probable energy of the molecules is given by making:

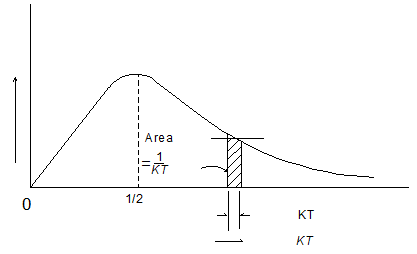
Fig. 4.22 Maxwell-Boltzmann energy distribution function

(4.164)

On simplification,

(4.165)