Differentiating this equation with respect to T (keeping P constant)

(G)

or

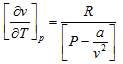
From Eqn. C

Plugging this value of P into Eqn. G, we get

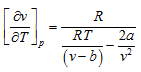
or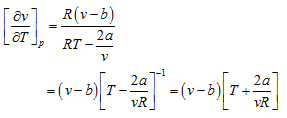 

or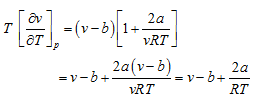 
or

Now, according to the J-T effect, the change in temperature is

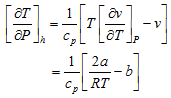
Therefore,
Since dP is always negative due to the J-T expansion, three cases arise:

Case 1: cooling effect (i.e., dT is negative) will be observed if
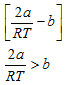 is positive, i.e., if

Case 2: heating effect (i.e., dT is positive) will be observed if
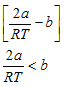is negative, i.e., if
Case 3: there will be neither a heating effect nor a cooling effect (i.e., dT = 0) if
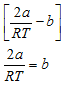 is zero

The temperature at which the J-T effect is zero is called the temperature of inversion (Ti), so