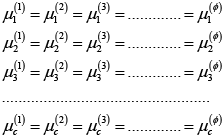Let us consider a heterogeneous system in which c constituents (i = 1,2,3,......,c) are present in all the phases. Initially we consider no chemical reaction to avoid the complexity. Let us assume that there are Φ phases. In each phase, all the constituents are present, i.e.,

Φ = 1, constituents are n1, n2,........, nc Φ = 2, constituents are n1, n2,........, nc ............................................. Φ = 5, constituents are n1, n2,........, nc

(2.172)

For ease of description we will identify the constituents by subscript and phase by superscript.

The Gibbs function of the whole heterogeneous system is

(2.173)

G = G (T,p,ni)

(2.174)

Since there is no chemical reaction, only way in which n's may change is by the transport of the constituents from one phase to another. In this case, the total number of moles of each constituent will remain constant.

.............................................

(2.175)

At chemical equilibrium, G will be rendered a minimum at constant T & P subject to the aforementioned equations of constraints.

∴ dGT,p = 0

(2.176)

Therefore, from the condition of equilibrium of a heterogeneous system (chemical equilibrium),

μij = μia

(2.177)

(2.178)