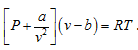Example 2:

Prove that heat at constant pressure is given by

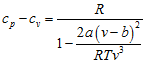
Solution:

the specific heat at constant pressure is given by

The specific heat at constant volume is given by

Therefore,

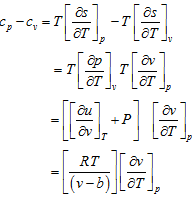
Differentiating van der Waals’ equation

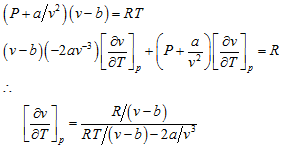
Substituting this value in the specific heat difference equation above,

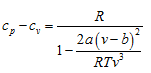
Example 3:

Joule-Thomson expansion apply to a van der Waals equation

For 1 mol of a real gas, the vander Waals equation takes the form

(C)

Where a and b are constants. Transposing

(D)

Or

(E)

Now, a and b are very small. So their product ab is very small compared to v2 and as such term can be neglected, whereupon the foregoing equation simplifies to

(F)