A short exact sequence of complexes (29.16) induces a long exact sequence in homology
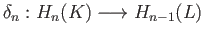
(29.17)
where the map
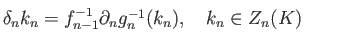 known as the connecting homomorphism is given by the formula
known as the connecting homomorphism is given by the formula
Here
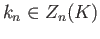 refers to the homology class of
refers to the homology class of
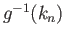 and
and
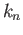 refers
to any pre-image of
refers
to any pre-image of 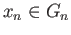 .
.
nisha
2012-03-20
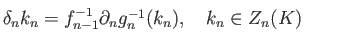 known as the connecting homomorphism is given by the formula
known as the connecting homomorphism is given by the formula