A short exact sequence of chain complexes consists of three chain complexes of abelian groups
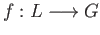 and
and  and chain maps
and chain maps
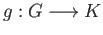 and
and
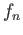 such that
such that
- (i)
- For each
 , the map
, the map 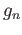 is injective.
is injective.
- (ii)
- For each
 , the map
, the map 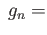 is surjective.
is surjective.
- (iii)
- For each
 , ker
, ker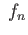 Im
Im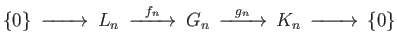 .
.
Thus for each  we have the diagram
we have the diagram
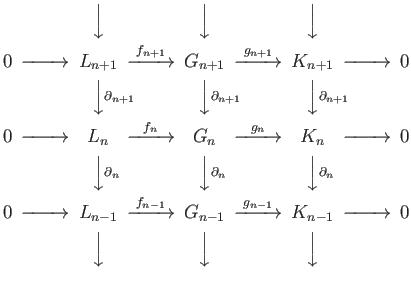
(29.16)
We now write out two more parallel rows with  replaced by
replaced by 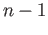 and
and 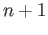 and the boundary maps
going across the rows:
We now state and prove the fundamental result.
and the boundary maps
going across the rows:
We now state and prove the fundamental result.
nisha
2012-03-20
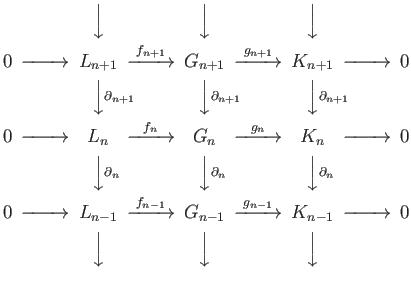 (29.16)
(29.16)