We must first show that displayed formula (29.18) gives a well-defined map since several
choices are being made. First, for
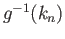 surjectivity of
surjectivity of 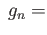 shows that there exists
shows that there exists
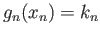 such that
such that
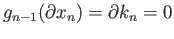 . Applying the boundary map
. Applying the boundary map
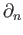 we see that
we see that
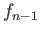 which, by virtue of exactness of (29.16) and injectivity of
which, by virtue of exactness of (29.16) and injectivity of 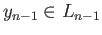 , shows there is a unique
, shows there is a unique
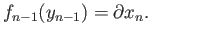 such that
such that
We have to now show that 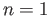 is a cycle in
is a cycle in 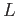 . This is clear if
. This is clear if 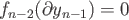 and so we assume
and so we assume 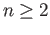 .
Applying the boundary map to (29.19) gives
.
Applying the boundary map to (29.19) gives
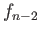 from which we conclude, since
from which we conclude, since 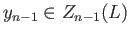 is injective, that
is injective, that
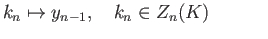 .
Hence the assignment
.
Hence the assignment
is well defined once we show that it is independent of the choice of
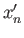 .
.
Second, we suppose that for a given
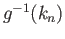 ,
,
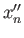 and
and
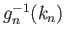 are two members of
are two members of
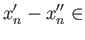 then
then
So there is a
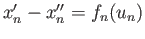 such that
such that
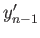 .
On the other hand, for these two choices there exist
.
On the other hand, for these two choices there exist
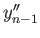 and
and
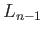 in
in 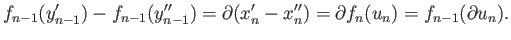 such that (29.19) holds and so
such that (29.19) holds and so
Injectivity of 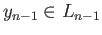 implies
implies
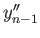 and
and
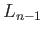 differ by a
boundary and so define the same homology class.
differ by a
boundary and so define the same homology class.
Third, we must show that the same homology class results if we begin with
two homologous cycles
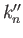 and
and
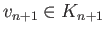 .
In this there exists
.
In this there exists
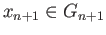 and
and
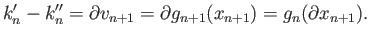 such that
such that
Let
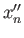 and
and
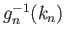 be chosen from
be chosen from
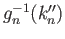 and
and
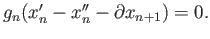 respectively so that
respectively so that
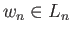 By exactness of (29.16) there is a
By exactness of (29.16) there is a
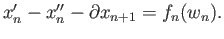 such that
such that
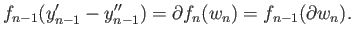 Applying
Applying 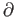 to this and and recalling (29.19) we see that the
corresponding cycles
to this and and recalling (29.19) we see that the
corresponding cycles
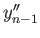 and
and
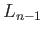 satisfy
satisfy
Since 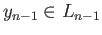 is injective we see that
the cycles
is injective we see that
the cycles
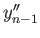 and
and
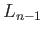 are homologous.
nisha
2012-03-20
are homologous.
nisha
2012-03-20
![]() ,
,
![]() and
and
![]() are two members of
are two members of
![]() then
then
![]() and
and
![]() .
In this there exists
.
In this there exists
![]() and
and
![]() such that
such that