(i) For a continuous map
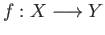 , the maps
, the maps
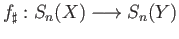 satisfy
satisfy
The
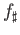 on the right hand side obviously refers to the map
on the right hand side obviously refers to the map
 and
and
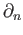 refers to the boundary operator on
refers to the boundary operator on 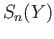 on the left hand side whereas it refers to the boundary operator on
on the left hand side whereas it refers to the boundary operator on
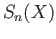 on the right hand side.
on the right hand side.
(ii) If
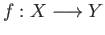 and
and
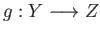 are two continuous maps then the maps
are two continuous maps then the maps
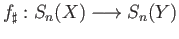 and
and
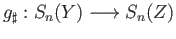 satisfy
satisfy
nisha
2012-03-20
![]() and
and
![]() are two continuous maps then the maps
are two continuous maps then the maps
![]() and
and
![]() satisfy
satisfy