Definition 29.4:

Given a continuous map 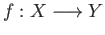$f : X \longrightarrow Y$, the map 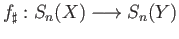$f_{\sharp}:S_n(X)\longrightarrow S_n(Y)$ is the group homomorphism which is defined on singular $n$ simplices $\sigma$ via the prescription

$$f_{\sharp}(\sigma) = f\circ \sigma, \eqno(29.6)$$

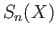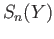and extended as a group homomorphism from $S_n(X)$ to $S_n(Y)$. We ought to denote this map by 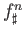$f^n_{\sharp}$ but we shall suppress the superscript to enhance readability.