It clearly suffices to check the result on the generators of 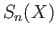 . So let
. So let  be
an arbitrary singular
be
an arbitrary singular  simplex. Using equation (29.4),
simplex. Using equation (29.4),
To use lemma (29.1) we break the double sum in two pieces and write
Using (29.2) in the second piece we get
It may be noted that each of the two pieces is a sum of 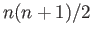 terms (why?).
Renaming
terms (why?).
Renaming 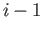 as
as 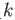 in the second sum gives
in the second sum gives
as desired.
Now suppose that  and
and  are two topological spaces and
are two topological spaces and
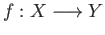 is a continuous map then
is a continuous map then
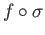 is a singular
is a singular 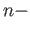 simplex in
simplex in  whenever
whenever  is a singular
is a singular 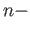 simplex in
simplex in  .
.
nisha
2012-03-20
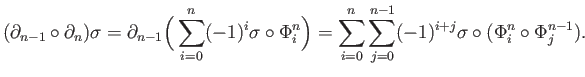
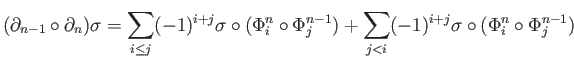
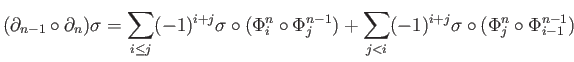
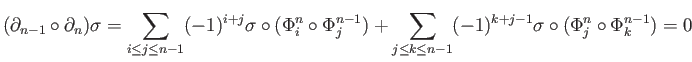
![]() and
and ![]() are two topological spaces and
are two topological spaces and
![]() is a continuous map then
is a continuous map then
![]() is a singular
is a singular ![]() simplex in
simplex in ![]() whenever
whenever ![]() is a singular
is a singular ![]() simplex in
simplex in ![]() .
.