Some motivation for singular homology:

Let us recall some of the notions in the theory of contour integrals in elementary complex analysis. Given a holomorphic function $f:\Omega\longrightarrow \mathbb{C}$ one defines a line integral

$$\int_{\gamma} f(z) dz \eqno(28.1)$$

along a path⁵ $\gamma:[a, b]\longrightarrow \Omega$ lying in the domain $\Omega$. If the path $\gamma$ is the juxtaposition of several paths $\gamma_1, \gamma_2, \dots, \gamma_k$ then one knows that

$$\int_{\gamma} f(z) dz = \int_{\gamma_1} f(z) dz + \int_{\gamma_2} f(z) dz + \dots + \int_{\gamma_k} f(z) dz\eqno(28.2)$$

Thus one can break the path $\gamma$ into several pieces, compute the integral over the individual pieces and add the results. One can also reparametrize the pieces and regard all the pieces $\gamma_j$ as being maps from $[0, 1]$. In view of all these, it seems meaningful to write

$$\gamma_1 + \gamma_2 + \dots + \gamma_k \eqno(28.3)$$

in place of

$$\gamma_1 * \gamma_2 * \dots * \gamma_k.$$

We see that the rigidity present in the theory of the fundamental group where one deals with homotopy classes of loops all of which are based at a given point, is now significantly relaxed.

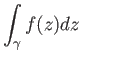
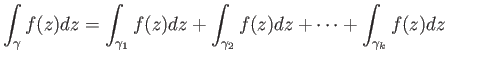
Also, one checks that integration along the inverse path reverses the sign:

$$\int_{\gamma^{-1}}f(z) dz = -\int_{\gamma}f(z) dz \eqno(28.4)$$

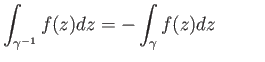
Taking a specific example with $f(z) = 1/z$ and integrating along two concentric circles $\gamma_1$, $\gamma_2$ traced counter clockwise, we see that

$$\int_{\gamma_1}f(z) dz = \int_{\gamma_2}f(z) dz. \eqno(28.5)$$

Using (28.1) and (28.4) this may be rewritten as

$$\int_{\gamma_1-\gamma_2}f(z) dz = 0, \eqno(28.6)$$

where, in keeping with the additive notation (28.3) we have written $-\gamma_2$ in place of $\gamma_2^{-1}$. Equation (28.6) is interesting since $\gamma_1$ and $\gamma_2$ are the two pieces of the boundary of the annular region $A$ bounded by them, where the function $f$ is holomorphic. Equation (28.6) suggests that the two paths $\gamma_1$ and $\gamma_2$ ought to be regarded as being equivalent with regard to $f$ or more precisely with regard to $A$ since nothing changes if $f$ is replaced by any other function holomorphic in an neighborhood of $A$. However (28.6) fails for $f(z) = (z-p)^{-1}$, where $p$ is any point in the interior of $A$. This is a reflection of the fact that the paths $\gamma_1$ and $\gamma_2$ do not constitute the full boundary of the punctured annulus $A - \{p\}$ which is where $(z-p)^{-1}$ is holomorphic.

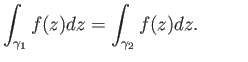
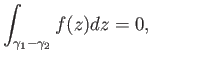
In doing contour integrals one occasionally introduces auxiliary paths such as $\sigma_j$ ($j = 1, 2$) indicated in the figure below and writes the integral (28.6) over $\gamma_1-\gamma_2$ as the sum

$$(\gamma_1^{\prime}+\sigma_1 - \gamma_2^{\prime} + \sigma_2) + (\gamma_1^{\prime\prime}-\sigma_1 - \gamma_2^{\prime\prime} - \sigma_2) \eqno(28.7)$$

in Each of the two parenthesis indicates a boundary of one of the halves of the annulus and so each ought to equivalent to a null path or in other words, the equivalence of $\gamma_1$ and $\gamma_2$ translates to $\gamma_1-\gamma_2$ being equivalent to a null path. We write $\gamma_1 \sim \gamma_2$ to indicate the equivalence of $\gamma_1-\gamma_2$ to a null-path.

These considerations suggest an underlying calculus of paths bounding regions in the plane. Indeed homology theory does develop such a calculus of paths as well as its higher dimensional analogues. Perhaps the student has encountered these higher dimensional analogues in connection with the Gauss' divergence theorem in vector calculus⁶.

Note that the sum indicated in (28.3) is a formal sum we are lead to the free abelian group generated by the set of all piecewise smooth functions from $[0, 1]$ to $\Omega$ called the group of one chains. Thus $\gamma_1-\gamma_2$ in (28.6) and $\gamma_1 + \gamma_2 + \dots + \gamma_k$ displayed in (28.3) are examples of one chains. Note that the one chain appearing in (28.2) is different from $\gamma$ though in the final stage of construction they would be identified. The Cauchy theory suggests that the chains whose pieces are all closed curves would play a distinguished role and these are examples of one cycles - a certain subgroup of the group of chains called the group of one cycles $Z_1$. If a chain such as $\gamma_1-\gamma_2$ appearing in equation (28.6) is the oriented boundary of a sub-domain we would regard it as being equivalent to zero and we would call such chains as boundaries. These form a subgroup of $Z_1$ known as the group of boundaries $B$. The equivalence relation is thus $\gamma_1 \sim \gamma_2$ if and only if $\gamma_1 - \gamma_2 \in B$. Passing to the quotient of $Z$ via this equivalence relation or in algebraic terms, passing to the quotient group $Z/B$ would give us the first homology group of the space $\Omega$. All these heuristics are rigorously defined in the next couple of lectures. We shall of course have to dispense with the notion of piecewise smoothness and talk of continuous paths $\gamma :[0, 1] \longrightarrow X$ called singular one simplexes and and their formal linear combinations with integer coefficients called singular one chains . To develop a calculus of higher dimensional chains, one has the option of introducing singular cubes namely continuous maps $[0, 1]^n \longrightarrow X$, which is the approach taken by W. Massey. This however necessitates certain preliminary reductions but has some distinct advantages later particularly in applications of homology theory to the study of homotopy groups. We shall follow the traditional approach, as in J. Vick's book and use singular simplices instead. in

Lectures - XXIX/XXX The singular chain complex and homology groups

in The program of developing a calculus of chains is now formalized in this lecture. We introduce a new algebraic category of chain complexes and maps between them and prove the fundamental theorem about these algebraic gadgets. In particular, to each chain complex is associated a sequence of groups called the homology groups. Given a topological space $X$ we associate a chain complex to it and obtain the homology functors from the category Top to the category AbGr. Thus we lay in this lecture the foundations for a systematic calculus of chains and cycles putting the heuristic ideas of the last lecture on a rigorous footing.