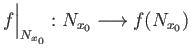- Suppose that
 is a finite group acting freely on a Hausdorff space then
the action is properly discontinuous and hence deduce that the group action in the example of the generalized
Lens space is properly discontinuous.
is a finite group acting freely on a Hausdorff space then
the action is properly discontinuous and hence deduce that the group action in the example of the generalized
Lens space is properly discontinuous.
- Suppose that
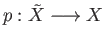 is a covering projection and
is a covering projection and
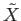 is locally path connected and simply connected.
Show that if
is locally path connected and simply connected.
Show that if  is an evenly covered open set in
is an evenly covered open set in  and
and
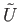 is a sheet lying above it then
is a sheet lying above it then
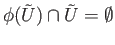 for every
for every
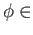 Deck
Deck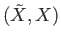 and
and 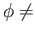 id
id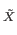 . Deduce that the
group of deck transformations acts properly discontinuously on
. Deduce that the
group of deck transformations acts properly discontinuously on
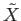 . How does this relate to theorem 17.2?
. How does this relate to theorem 17.2?
- Does the fundamental group of Klein's bottle have elements of finite order? Identify this group
with a familiar group that we have already encountered in lecture 7. What is its abelianization?
- Show that the torus is obtained as the orbit space of a group of homeomorphisms acting properly discontinuously on
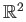 .
Write out these homeomorphisms explicitly.
.
Write out these homeomorphisms explicitly.
- Show that the torus is a double cover of the Klein's bottle. Hence the fundamental group of the Klein's bottle must contain a
subgroup of index two. Determine this subgroup.
- Show that the cylinder is a two-sheeted cover of the Möbius band.
- Suppose that
 is a topological group,
is a topological group,  is a discrete subgroup of
is a discrete subgroup of  . Show that there exists a neighborhood
. Show that there exists a neighborhood  of the identity such that
of the identity such that
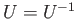 ,
,
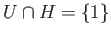 and that
and that
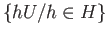 is a family of disjoint open sets. Deduce that the quotient map
is a family of disjoint open sets. Deduce that the quotient map
 is a covering projection. Also show that
is a covering projection. Also show that  is Hausdorff.
is Hausdorff.
in
Lecture XXI - Test - III
in
- Show that a homeomorphism of
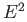 onto itself must preserve the boundary. That is it must map a boundary point to a
boundary point.
onto itself must preserve the boundary. That is it must map a boundary point to a
boundary point.
- Is it true that
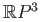 minus a point deformation retracts to a space homeomorphic to
minus a point deformation retracts to a space homeomorphic to
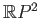 ?
?
- Let
 be the infinite grid
be the infinite grid

or
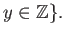
Consider the covering map from  onto the figure eight loop
onto the figure eight loop
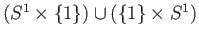 given by
given by
Determine the deck transformations of this covering. Is this a regular covering?
- Given topological spaces
 and
and  , a map
, a map
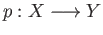 is said to be a local homeomorphism if
each
is said to be a local homeomorphism if
each 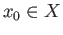 has a neighborhood
has a neighborhood 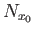 such that the restriction map
such that the restriction map
is a homeomorphism. Show that a local homeomorphism which is a proper map is a covering projection.
- Show that the map
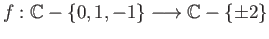 is a local homeomorphism. Is this map a covering projection? If so what is the group of deck transformations?
is a local homeomorphism. Is this map a covering projection? If so what is the group of deck transformations?
in
Lecture XXII - Fundamental group of
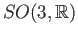 and
and
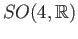
For many applications, it is important to know The fundamental groups of the classical groups.
We shall discuss in detail
the orthogonal groups
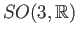 and
and
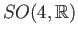 since their underlying topological
spaces are easily described. Indeed
since their underlying topological
spaces are easily described. Indeed
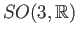 is the three dimensional real projective space and
is the three dimensional real projective space and
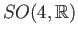 ,
as a topological space, is the product of the
three dimensional real projective space and the three dimensional sphere
,
as a topological space, is the product of the
three dimensional real projective space and the three dimensional sphere 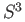 . To unravel the structure of
these spaces it is convenient to use quaternions.
We shall assume some basic familiarity with quaternions (see [1]).
We shall also use some basic facts from multi-variable calculus.
The student who is unfamiliar with these parts of
multi-variable calculus may omit these parts of the proof.
. To unravel the structure of
these spaces it is convenient to use quaternions.
We shall assume some basic familiarity with quaternions (see [1]).
We shall also use some basic facts from multi-variable calculus.
The student who is unfamiliar with these parts of
multi-variable calculus may omit these parts of the proof.
Subsections
nisha
2012-03-20