We show that the map
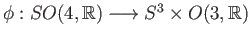 given by
given by
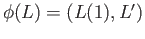 ,
where
,
where
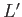 is defined as in the previous lemma, is a homeomorphism.
The map
is defined as in the previous lemma, is a homeomorphism.
The map
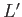 is an element of
is an element of
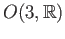 since it maps
since it maps 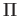 to itself and
preserves Euclidean norm. Further,
to itself and
preserves Euclidean norm. Further, 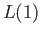 is obviously a unit quaternion. The image of
is obviously a unit quaternion. The image of  is a compact connected subspace
of
is a compact connected subspace
of
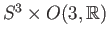 and
sends the identity element to the pair
and
sends the identity element to the pair
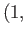 id
id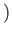 which means the image must be contained
in
which means the image must be contained
in
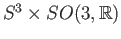 .
It is an exercise that the map is bijective. Since the space
.
It is an exercise that the map is bijective. Since the space
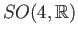 is compact and
is compact and
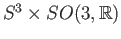 is Hausdorff,
it follows that
is Hausdorff,
it follows that  is a homeomorphism.
is a homeomorphism.
nisha
2012-03-20