The curves
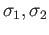 and
and 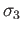 given by
given by
lie on 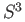 and pass through the point
and pass through the point  . Differentiating and setting
. Differentiating and setting 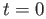 confirms that the vectors
confirms that the vectors
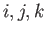 span the tangent space to
span the tangent space to 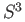 at
at 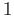 . Thus
. Thus
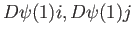 and
and 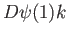 span the image of
span the image of 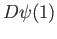 . We leave it to the reader to check, by calculating
the derivatives of
. We leave it to the reader to check, by calculating
the derivatives of
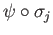 (
(
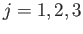 ) at
) at 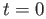 , that
, that
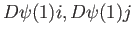 and
and 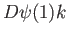 are linearly independent.
are linearly independent.
nisha
2012-03-20