- Recast the notion of homotopy of paths in terms of morphisms of the category
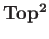 .
.
- Define a binary operation on
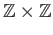 as follows
as follows
Show that this defines a group operation on
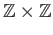 and this group is called the semi-direct
product of
and this group is called the semi-direct
product of
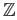 with itself. The standard notation for this is
with itself. The standard notation for this is
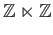 . Compute the inverse of
. Compute the inverse of 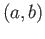 , compute
the conjugate of
, compute
the conjugate of 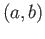 by
by 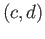 and the commutator of two elements. Determine the commutator subgroup and the
the abelianization of
and the commutator of two elements. Determine the commutator subgroup and the
the abelianization of
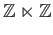 .
.
- A morphism
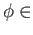 Mor
Mor in a category is said to be an equivalence if there exists
in a category is said to be an equivalence if there exists
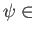 Mor
Mor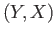 such that
such that
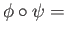 id
id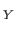 and
and
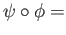 id
id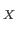 .
In a category whose objects are sets and morphisms are maps,
show that if
.
In a category whose objects are sets and morphisms are maps,
show that if 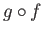 is an equivalence for
is an equivalence for
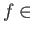 Mor
Mor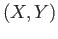 and
and
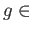 Mor
Mor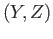 then
then 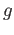 is surjective and
is surjective and  is injective.
is injective.
- We say a category
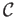 admits finite products if for every pair of objects
admits finite products if for every pair of objects 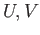 in
in 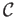 there exists an
object
there exists an
object 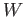 and a pair of morphisms
and a pair of morphisms
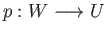 ,
,
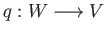 such that the following
property holds. For every pair of morphisms
such that the following
property holds. For every pair of morphisms
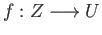 ,
,
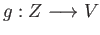 there exists a
unique morphism
there exists a
unique morphism
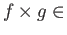 Mor
Mor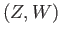 such that
such that
Show that the categories  ,
, 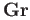 and
and
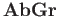 admit finite products and in fact the usual
product of topological spaces/groups serve the purpose with
admit finite products and in fact the usual
product of topological spaces/groups serve the purpose with  and
and 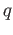 being the two projection maps.
being the two projection maps.
- Discuss arbitrary products in a category generalizing the preceding exercise and discuss the existence of arbitrary
products in the categories Top, Gr and AbGr.
- We say a category
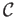 admits finite coproducts if for every pair of objects
admits finite coproducts if for every pair of objects 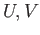 in
in 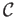 there exists an
object
there exists an
object 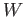 and a pair of morphisms
and a pair of morphisms
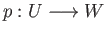 ,
,
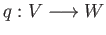 such that the following
property holds. For every pair of morphisms
such that the following
property holds. For every pair of morphisms
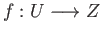 ,
,
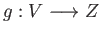 there exists a
unique morphism
there exists a
unique morphism
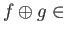 Mor
Mor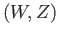 such that
such that
Show that the category
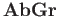 admits finite coproducts and in fact the usual
product of groups serves the purpose where the maps
admits finite coproducts and in fact the usual
product of groups serves the purpose where the maps  and
and 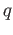 are the canonical injections:
are the canonical injections:
What happens when this (naive construction) is tried out in the category 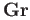 instead of
instead of
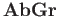 ?
In the context of abelian groups the coproduct is referred to as the direct sum.
?
In the context of abelian groups the coproduct is referred to as the direct sum.
- Discuss the coproduct of an arbitrary family of objects in the category AbGr.
It is referred to as the direct sum of the family.
- Suppose that
 and
and  are two topological spaces, form their disjoint union
are two topological spaces, form their disjoint union 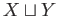 which is the set theoretic union of
their homeomorphic copies
which is the set theoretic union of
their homeomorphic copies
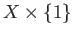 and
and
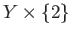 . A subset
. A subset  of
of 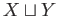 is declared open if
is declared open if
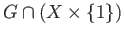 and
and
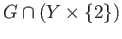 are both open. Check that this defines a topology on
are both open. Check that this defines a topology on
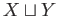 and the maps
and the maps
are both continuous. Show that the category  admits finite coproducts.
admits finite coproducts.
in
Lecture IX - Functorial Property of the Fundamental Group
We now turn to the most basic functor in algebraic topology namely, the 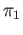 functor.
Recall that the fundamental group of a space involves a base point and according to
theorem (7.8) the fundamental
group of a path connected space is unique upto isomorphism. However, this isomorphism is not
canonical as theorem 7.9 shows and isomorphism classes of groups do not form a category. To get around this
difficulty and to obtain a well-defined functor, we introduce the category of pointed topological spaces.
functor.
Recall that the fundamental group of a space involves a base point and according to
theorem (7.8) the fundamental
group of a path connected space is unique upto isomorphism. However, this isomorphism is not
canonical as theorem 7.9 shows and isomorphism classes of groups do not form a category. To get around this
difficulty and to obtain a well-defined functor, we introduce the category of pointed topological spaces.
Subsections
nisha
2012-03-20