Let 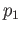 and
and 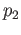 be the usual
projection maps
be the usual
projection maps
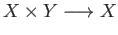 and
and
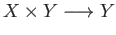 respectively and
respectively and  be a loop in
be a loop in 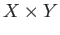 based at
based at
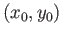 .
Then
.
Then
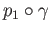 and
and
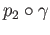 are loops in
are loops in  and
and  based at
based at  and
and 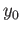 respectively.
The map
respectively.
The map
is well-defined and easily seen to be a surjective group homomorphism. Injectivity is also easy to check. Well,
suppose that ![$ [\gamma]$](img28.png) is in the kernel of
is in the kernel of  then
then
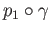 and
and
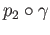 are homotopic to
the constant loops
are homotopic to
the constant loops
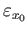 and
and
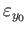 respectively via homotopies
respectively via homotopies 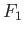 and
and 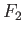 .
That is to say there exists continuous maps
.
That is to say there exists continuous maps
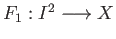 and
and
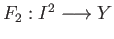 such that
such that
and
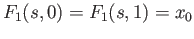 ,
,
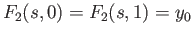 for all
for all
![$ s\in [0,1]$](img478.png) . Putting these
together we get a continuous map
. Putting these
together we get a continuous map
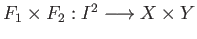 namely
namely
which is a homotopy between  and the constant loop at
and the constant loop at
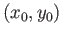 proving that the kernel is trivial.
nisha
2012-03-20
proving that the kernel is trivial.
nisha
2012-03-20