Suppose that
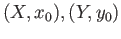 and
and 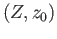 are pointed topological spaces. Let
are pointed topological spaces. Let
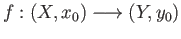 and
and
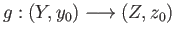 be continuous maps of pairs, that is continuous maps satisfying
be continuous maps of pairs, that is continuous maps satisfying
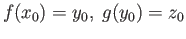 , then
the induced homomorphisms on the respective fundamental groups satisfies
, then
the induced homomorphisms on the respective fundamental groups satisfies
If
id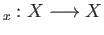 is the identity map then
is the identity map then
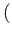 id
id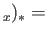 id
id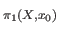 . That is to say,
the identity map on
. That is to say,
the identity map on 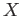 induces the identity homomorphism on
induces the identity homomorphism on
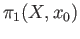 .
.
nisha
2012-03-20