This category will be denoted by
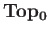 and its objects consists of all pairs
and its objects consists of all pairs 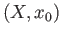 where
where  is a topological space and
is a topological space and  is a point of
is a point of  .
Given two pairs of pointed spaces
.
Given two pairs of pointed spaces 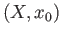 and
and 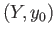 , the morphisms between them consists of
all continuous functions
, the morphisms between them consists of
all continuous functions
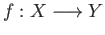 such that
such that
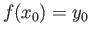 .
.
Suppose that 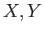 are path connected spaces and
are path connected spaces and
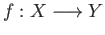 is a continuous map
such that
is a continuous map
such that
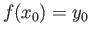 then
then  clearly defines a morphism, denoted by same letter, between pointed spaces
clearly defines a morphism, denoted by same letter, between pointed spaces
The map
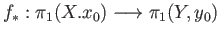 given by
given by
![$ f_*([\gamma]) = [f\circ\gamma ]$](img748.png) where
where  in
in  based at
based at  , is well defined since
, is well defined since
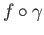 is a loop in
is a loop in  based at
based at 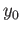 Therefore
Therefore 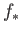 is well defined because if
is well defined because if
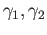 are homotopic loops in
are homotopic loops in  based at
based at  and
and 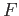 is the homotopy then
is the homotopy then 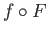 is a homotopy between
is a homotopy between
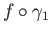 and
and
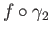 in
in  .
It is immediately checked that
.
It is immediately checked that
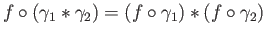 thereby giving a group homomorphism:
thereby giving a group homomorphism:
The group homomorphism 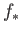 is called the map induced by
is called the map induced by  on the fundamental groups. In other words we
obtain a functor
on the fundamental groups. In other words we
obtain a functor 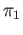 from
from
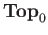 to
to 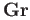 .
nisha
2012-03-20
.
nisha
2012-03-20
![]() are path connected spaces and
are path connected spaces and
![]() is a continuous map
such that
is a continuous map
such that
![]() then
then ![]() clearly defines a morphism, denoted by same letter, between pointed spaces
clearly defines a morphism, denoted by same letter, between pointed spaces