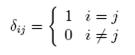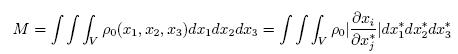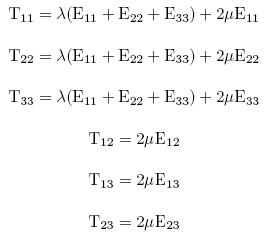MODULE 3: Indicial Notations, Tensors and Constitutive Equations

Lectures 11 – 14:

• Indicial Notations, Introduction to Tensors,
• Properties and examples of Tensors,
• Stress and Strain Tensors,
• Governing equations of Elasticity in Tensorial Notations,
• Constitutive Equations in Tensorial Notations

Keys-Words:  Tensors, Elasticity equations in Tensorial Notations, Constitutive equations in Tensorial Notations
 
Introduction
Stress and strain are key concepts in the analytical characterization of the mechanical state of a solid body. While stress represents internal forces per unit area resulting from loads applied to the body, strain is the resulting relative displacement of points in the body. This chapter formally introduces the notions of stress and strain tensors and it also shows how the mechanical equilibrium equations can be obtained directly from the application of the principle of virtual work. The chapter starts with a review of vectors and tensors.
Overview of Vectors and Tensors
Tensors are widely used in engineering analysis to denote physical quantities of interest. This section reviews basic notions of tensor analysis needed in continuum mechanics.
Notation
Tensors are important in applications because governing equations which have general va­lidity with respect to any frame of reference can be constructed by ensuring that every term in the equation has the same tensor characteristics. Thus tensor characteristics play a role analogous to that of dimensional analysis. Thus, once a physical quantity has been given the characteristic of a tensor then the components of the quantity can be transformed from one coordinate system to another according to the above rules.

In vector and tensor calculus, subscript and superscript index notation is used to denote collections of variables, for instance, the set  is denoted by  or by . Likewise, the set  is denoted as . Note that the superscript is just an index, not a power. If a power is meant, the quantity will be enclosed in parenthesis.
The summation convention is used to simplify the writing of equations consisting of col­lection of similar looking terms. Whenever a sum involving two identically indexed variables appears one simply writes a single term using a dummy index and omits the summation sign. For instance

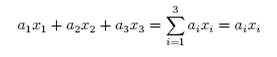………………..(1)

The summation convention also applies to derivatives, specifically, for a function  the total differential expressed in terms of the partial derivatives is

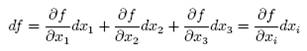………………..(2)

A concrete example is provided by the unit vector u in three dimensional Euclidean space in rectangular Cartesian coordinates. In tensor analysis, components are denoted by indices, so instead of writing x,y,z for the three coordinates in such space one writes .

………………..(3)

where  are the components of u and  are the unit coordinate vectors (i, j,k in rectangular Cartesian coordinates, respectively). The magnitude of , is given by

………………..(4)

Therefore, the dot product of two vectors a,b can be expressed as

………………..(5)

The quantity

is Kronecker’s delta. Another example is the differential arc or line element of a curve in space ds, this is

………………..(7)

where two summations are involved. Another example is the determinant of a 3 × 3 matrix |, this is given as

………………..(8)

where  is the permutation symbol defined as

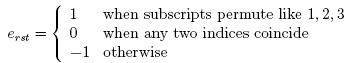………………..(9)

The permutation symbol and Kronecker’s delta are related by

………………..(10)

With the above, the vector product of two vectors can be simply expressed as

………………..(11)

The Euclidian Metric Tensor

Consider a system of rectangular coordinates. Consider also a new system of coordinates . The two systems being related by the expressions

………………..(12)

or

………………..(13)

so that to every triplet  there corresponds a triplet .

In any system of coordinates, coordinate curves in space are generated by varying one coordinate while holding the other two constant. If the three coordinate curves resulting from the triplet  are mutually perpendicular at each point P , then the triplet constitutes a system of orthogonal curvilinear coordinates.
 
If a differential segment of an arbitrary curve in space is associated with differential displacements in the coordinates  then it can be expressed as differential element of arc of a curve in coordinates  is

………………..(14)

 
But

therefore

where the functions

………………..(17)

are the components of the Euclidian metric tensor in the coordinate system .

Scalars, Vectors and Tensors

Scalars, vectors and tensors are mathematical entities that are used in applications to rep­resent meaningful physical quantities. Consider two systems of coordinates  and  which are related by the coordinate transformation rules described above. Physical quantities of interest can be represented in any of these two systems. A scalar is an entity consisting of a single component and is represented in terms of  by the single component (number) ¢ and in terms of by. If the two numbers are one and the same

A scalar is also considered a tensor of rank or order zero.

A contravariant tensor is a tensor having specific transformation properties of, a covariant tensor. A covariant tensor, denoted with a lowered index (e.g., ) is a tensor having specific transformation properties. In general, these transformation properties differ from those of a contravariant tensor.
If an entity has instead three components in each of the coordinate systems is called a contravariant vector or contravariant tensor of order one and individual components and  in the two systems are related by

………………..(19)

The use of the index as superscript distinguishes contravariant vectors.
 
Likewise, if an entity has three components in each of the coordinate systems is called a covariant vector or covariant tensor of rank or order one and individual components and in the two systems are related by

………………..(20)

The use of the index as subscript distinguishes contravariant vectors. Covariant and con­travariant components are identical in rectangular Cartesian systems of coordinates but they are not in curvilinear coordinates. By convention, only the subscript index notation is used to describe vectors in rectangular Cartesian systems of coordinates.

Now, if an entity has nine components one has tensor of rank or order two. There are also contravariant and covariant tensors which transform according to

………………..(21)

and

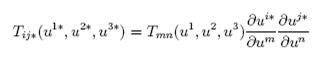………………..(22)

respectively.
Mixed tensor fields of rank two can also be defined as well as tensors of higher ranks.

Again, in rectangular Cartesian systems of coordinates, there is no distinction between contravariant and covariant tensors. By convention only the subscript index notation is used to describe tensors in rectangular Cartesian systems of coordinates.
The Kronecker delta defined before can be regarded as a component of a rank two tensor which turns out to be the Euclidian metric tensor , while the permutation symbol can be regarded as a component of a rank three tensor called the permutation tensor or the alternator .

It should be noted that given a tensor, others can be generated from it by a process called contraction which consists of equating and summing a covariant and a contravariant index of a mixed tensor.

Algebraic Properties of Second Order Tensors

Recall that tensors, just as vectors can be added (each component of the resulting tensor is the sum of the corresponding components in the original tensors). They can also be multiplied according to the rule

………………..(23)

Also, tensors are symmetric if and antisymmetric if .

A vector can be obtained from a tensor  and an arbitrary vector by multiplication as follows

………………..(24)

The new vector B has generally different magnitude and direction from A. Now, if , where is a scalar, it is called the characteristic vector of and the directions associated with it are called the characteristic or principal directions of . The axes determined by the principal directions are called the principal axes of . The problem of finding the principal axes of a tensor is called the reduction of to principal axes. The components of A determining the principal axes of  satisfy the system of equations

………………..(25)

This system has a nontrivial solution only when the determinant
 

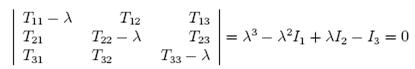………………..(26)

where the quantities

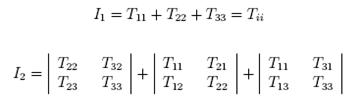………………..(27)

and

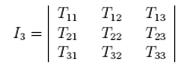………………..(28)

are called the invariants of the tensor .
The equation

………………..(29)

is called the characteristic equation for the determination of the eigen values of a tensor.

Partial Derivatives in Cartesian Coordinates

In Cartesian coordinates, the partial derivatives of any tensor field are the components of an­other tensor field. Consider two Cartesian systems of coordinates and related by the rule
 

………………..(30)

where  and are constants. Let  be a contravariant tensor so that

………………..(31)

then one has the relationship

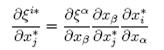………………..(32)

i.e. the partial derivatives of  transform as a rank two tensor in Cartesian coordinates. This is not the case in curvilinear coordinate systems.

The comma notation is often used to denote partial derivatives. For instance the tensors  and  are of rank one, two and three, respectively assuming that  and are tensors of ranks zero, one and two, respectively.

Further, the covariant derivative of the covariant vector is defined as

………………..(33)

and they are the components of a covariant tensor of rank two. Here, the quantity

………………..(34)

is called the Euclidian Christoffel symbol.

Characteristics of Tensor Equations

The key property of tensor fields is that if all the components of a tensor vanish in a given co­ordinate system, they also vanish in all other systems obtainable from the first by admissible transformations. As a consequence, a tensor equation established in one coordinate system will also hold in any other system obtainable from the first by admissible transformations.

For instance, the mass contained inside a given volume V is

 
Also the total volume contained inside a closed surface is

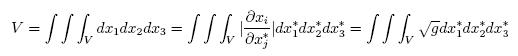……..(36)

Geometric Interpretation of Tensor Components

Recall that the set of unit vectors or base vectors,  for  in Euclidean space is a set of linearly independent vectors such that any vector in the space can be generated from them by simple linear combination. Consider an infinitesimal vector connecting two closely placed points in space referred to a Cartesian coordinate system. In a new and arbitrary coordinate system , the same vector is represented as

……..(37)

where  is the covariant base vector and is the contravariant base vector. Moreover,

……..(38)

so that represents the change in the position vector r with and points along the tangent to the coordinate curve.

It can be shown that and .

A vector v can then be expressed

……..(39)

and the contravariant components  of v are the components in the direction of the covariant base vectors and vice versa.

Consider two coordinate systems. The associated base vectors are and .

Then, the transformation laws for a vector are

……..(40)

and

……..(41)

Likewise, in the case of tensors of rank two the transformation laws are

……..(42)

and

……..(43)

Constitutive Equations in tensorial Notions

Linear Elastic Relation

In this section we study the relation between stress and strain in the context of linear elasticity. A constitutive equation relates the stress to relevant quantities of deformation. We assume that deformations are small and the rate of load application has no effect. In general, we can, therefore, write:

with T(0) = 0. We assume the function T(E) to be linear in this section, so we can write the general linear constitutive relation as follows:

where are the components of a fourth-order tensor called the elasticitytensor. This tensor is characteristic of anisotropic Hookean elastic solids.

A material is called isotropic if its mechanical properties are independent of direction. On the other hand, a material is called anisotropic if its mechanical properties are dependent on direction. Therefore, for an isotropic material, the components of the elasticity tensor must be independent of the rotation and reflection of the rectangular basis, i.e., for all orthogonal transformations of basis. Such a tensor is called an isotropic tensor. In general,  can be written in terms of isotropic tensors as follows:

where and  are isotropic tensors.

By substituting value in , we obtain:

……..(47)

. Let , then above equation becomes:

Or

……..(49)

The two material constants λ and µ are called Lame’s constants. In expanded form, equations (85) in module-2 are the constitutive equations for linear isotropic elastic solids, given as follows:

Hyperlinks for further details:

• Hyperlink-1
• Hyperlink-2
• Hyperlink-3
• Hyperlink-4
• Hyperlink-5