Now putting the expressions of ‘BV₁' and ‘D₂' from equation (3.26) and equation (3.27) respectively in above expression results in the following;

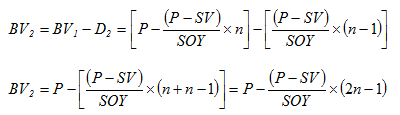(3.28)

Similarly the expressions for depreciation and book value for 3^rd year are presented below.

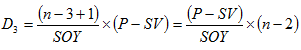(3.29)

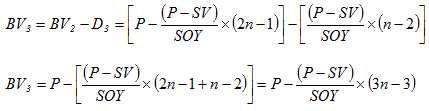(3.30)

The expressions for depreciation and book value for 4^th year are given by;

(3.31)

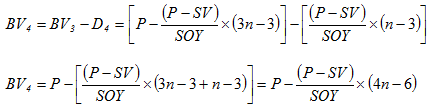(3.32)

Similarly the expressions for depreciation and book value for 5^th year are given by;

(3.33)

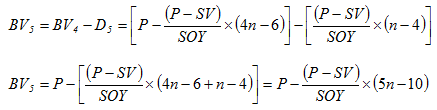(3.34)

The expressions for book value in different years are presented above to find out the generalized expression for book value at end of any given year. Now referring to the expressions of book values BV₁ , BV₂ , BV₃ , BV₄ , BV₅ in above mentioned equations, it is observed that the variable terms are ‘n ', ‘(2n- 1)', ‘(3n -3)', ‘(4n-6)' and ‘(5n-10)' respectively. These variable terms can also be written ‘(n +1- 1 )', ‘(2n+1 - 2 )', ‘(3n +1- 4 )', ‘(4n+1- 7 )' and ‘(5n+1- 11 )' respectively. The numbers 1, 2, 4, 7, and 11 in these variable terms follow a series and it is observed that value of each term is equal to value of previous term plus the difference in the values of current term and previous term. On this note, the general expression for value of ‘m ' term of this series is given by;

(3.35)

Now the generalized expression for book value for any year ‘m ' is given by;

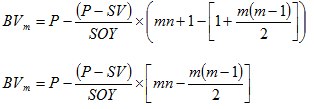(3.36)

In this method also, the annual depreciation during early years is more as compared to that in later years of the asset's useful life.