| |
Fig. 6.12a shows a typical trapezoidal section of a gravity retaining wall.
The forces acting on the wall per unit length are: |
 |
The weight of the wall ( 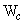 ) ) |
 |
The Resultant soil reaction R on the base. (or Resultant of weight 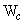 & & 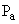 ).Strike the base at point D. There is equal and opposite reaction R' at the base between the wall and the foundation. ).Strike the base at point D. There is equal and opposite reaction R' at the base between the wall and the foundation. |
 |
Passive earth pressure 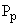 acting on the lower portion of the face of the wall, which usually small and usually neglected for design purposes. The full mobilization of passive earth pressure not occurs at the time of failure so we not consider it. If we consider it then it shows resistance against instability. So if we ignore it then we will be in safer side. acting on the lower portion of the face of the wall, which usually small and usually neglected for design purposes. The full mobilization of passive earth pressure not occurs at the time of failure so we not consider it. If we consider it then it shows resistance against instability. So if we ignore it then we will be in safer side. |
| |
First decide which theory we want to apply for calculating the active earth pressure. Normally we calculate earth pressure using Rankine's theory or Coulomb's Earth pressure theory.
For using Rankine's theory, a vertical line AB is drawn through the heel point
( Fig 6.12-b ). It is assumed that the Rankine active condition exist along the vertical line AB. While checking the stability, the weight of the soil ( 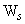 ) above the heel in the zone ABC should also be taken in to consideration, in addition to the Earth pressure ( ) above the heel in the zone ABC should also be taken in to consideration, in addition to the Earth pressure ( 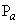 ) and weight of the wall ( ) and weight of the wall ( 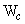 ). ).
But Coulomb's theory gives directly the lateral pressure ( 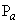 ) on the back face of the wall, the forces to be considered only ) on the back face of the wall, the forces to be considered only 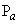 (Coulomb) and the Weight of the wall ( (Coulomb) and the Weight of the wall ( 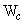 ). In this case, the weight of soil ( ). In this case, the weight of soil ( 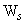 ) is need not be considered. ) is need not be considered.
Once the forces acting on the wall have been determined, the Stability is checked using the procedure discussed in the proceeding section. For convenience, the section of the retaining wall is divided in to rectangles & triangles for the computation of the Weight and the determination of the line of action of the Weight. |