| |
| | |
|
A segment of undivided four-lane highway on level terrain has field-measured
FFS 74.0-km/h, lane width 3.4-m, peak-hour volume 1,900-veh/h, 13 percent
trucks and buses, 2 percent RVs, and 0.90 PHF.
What is the peak-hour LOS, speed, and density for the level terrain portion of
the highway?
The solution steps are given below:
- Data given:
Level terrain,
field measured FFS = 74 km/h,
lane width is 3.4 m,
peak-hour volume = 1900 veh/h,
percent trucks and buses pt = 0.13,
percent RVs PR = 0.02, and
PHF=0.90.
- Determination of flow rate(Vp):
LOS can be calculated by knowing flow rate and free flow speed.
Flow rate (Vp) is calculated from the equation
Since 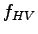 is unknown it is calculated from the equation is unknown it is calculated from the equation
where,
ET and ER are passenger-car equivalents for trucks and buses and for recreational
vehicles (RVs) respectively
PT and PR are proportion of trucks and buses, and RVs, respectively, in the
traffic stream (expressed as a decimal fraction)
Assume no RVs, since none is indicated.
- Determination of free flow speed(S):
In this example the free flow speed (FFS) measured at the field is given and hence
no need to compute free flow speed by indirect method.
Therefore,
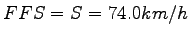 . .
- Determination of density(D):
The density of flow is computed from the equation
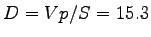
- Determination of LOS:
LOS determined from the speed-flow diagram.
LOS = C.
|
|
| | |
|
|
|