| |
| | |
|
A 10 km long 4 lane undivided multilane highway in a suburban area has a
segment 1 km long with a 3% upgrade and a segment 1 km long with a 3%
downgrade.
The section has a volume of 1900 vehicles/hr in each direction with 13% trucks
and buses and 2% recreational vehicles.
The 85 th percentile speed of passenger car is 80 km/hr on upgrade and 86km/hr
on downgrade.
There are total of 12 access points on both sides of the roadway.
The lane width is 3.6 m, PHF is 0.90 and having a 3m lateral clearance.
Determine the LOS of the highway section (upgrade and downgrade) during the
peak hour?
From HCM,
For a 3% upgrade and 1 km length( ET=1.5 , ER=3)
For a 3% downgrade and 1 km length( ET=1.5 , ER=1.2 )
- Data given:
3%upgrade and 3%downgrade
No of lanes = 4, N = 4,
80.0 km/h 85th-percentile speed for upgrade,
86 km/h 85t h-percentile speed for downgrade,
3.6-m lane width,
1,900-veh/h peak-hour volume, (V =1900 veh/h)
13 % trucks and buses, (PT =0.13)
2 % Recreational vehicles, ( Pr=0.02 )
12 access points/km,
PHF = 0.90
lateral clearance = 3 m
- Determination of flow rate(VP):
LOS can be calculated by knowing flow rate and free flow speed.
For upgrade:
Flow rate is calculated from the equation
where, Vp = 15-min passenger-car equivalent flow rate (pc/h/ln), V = hourly
volume (veh/h), PHF = peak-hour factor, N = number of lanes, fHV =
heavy-vehicle adjustment factor, and fp = driver population factor
Since fHV is unknown it is calculated from the equation
where,
ET and ER = passenger-car equivalents for trucks and buses and for recreational
vehicles (RVs), respectively
PT and PR = proportion of trucks and buses, and RVs, respectively, in the
traffic stream (expressed as a decimal fraction)
Assume no RVs, since none is indicated.
For downgrade:
- Determination of free flow speed(S):
For upgrade:
BFFS is approximately equal to 62.4 km/h when the 85 th percentile speed is 64
km/h, and it is 91.2 km/h when the 85 th percentile speed is 96 km/h and the in
between speed values is found out by interpolation.
Hence for 86 km/hr
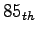 percentile speed from interpolation we get,
BFFS = 77.0 km/h
Now, Compute east bound and west bound free-flow speeds percentile speed from interpolation we get,
BFFS = 77.0 km/h
Now, Compute east bound and west bound free-flow speeds
For downgrade:
BFFS is approximately equal to 62.4 km/h when the 85 th percentile speed is 64
km/h, and it is 91.2 km/h when the 85 th percentile speed is 96 km/h and the in
between speed values is found out by interpolation.
Hence for 86 km/hr 85th percentile speed from interpolation we get,
BFFS= 82.0 km/h
Now, Compute the free-flow speed
- Determination of LOS
LOS determined from the speed-flow diagram.
LOS = D (for upgrade)
LOS = D (for downgrade)
|
|
| | |
|
|
|