Step 5.   Examine the first column,

• a.  A system is stable if all the above elements in the first column of the Routh Array are positive

b.  If any one of the elements of first column is negative, we have at least one pole at the right hand side of the imaginary axis and the closed loop system is unstable

c.  The number of times the sign changes (from positive to negative to positive again and so on) indicates the number of unstable poles present in the closed loop system

The last example (Eq. IV.42) can be revisited with Routh Hurwitz criterion. The polynomial coefficients, can be written in a Routh Array,

                                                     Table IV.2: Routh Array of eq. (IV.42)

The first column of the Routh array is . Hence the system has unstable pole(s). The sign is changed twice in the column (positive to negative and then negative to positive). Hence the closed loop system has two unstable poles .

The Routh Array can also be used for finding the stability limits of the controller parameters.

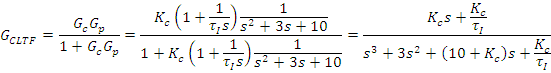(IV.45)