Estimation of Boundary Layer Parameters
Boundary layer thickness 
: It is defined as the distance away from the wall at which the velocity component parallel to the wall is 99% of the fluid speed outside the boundary layer. From Table 5.9.1, it is seen that 
. So, replacing 
in Eq. (5.9.4), one can obtain the following expression for boundary layer thickness;
 |
|
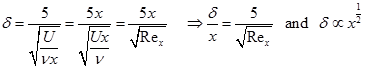At this point, the transverse velocity can be calculated from Eq. (5.9.8).
 |
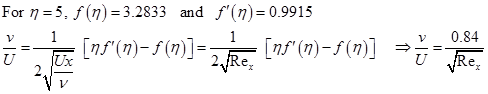(5.9.14) |
Displacement thickness 
: It is the distance that a streamline just outside of the boundary layer is deflected away from the wall due to the effect of the boundary layer. Mathematically, it can be represented in terms of transformed variable using Eq. (5.9.4).
 |
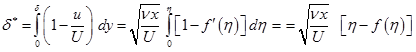(5.9.15) |
It may be seen from the Table 5.9.1 that for all values of 
, the functional value of Eq. (5.9.15) is always a constant quantity i.e. 
. So, Eq. (5.9.15) can be simplified in terms of Reynolds number;
 |
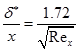(5.9.16) |
Momentum thickness 
: It is defined as the loss of momentum flux per unit width divided by 
due to the presence of the growing boundary layer. Mathematically, it can be represented in terms of transformed variable using Eq. (5.9.4).
 |
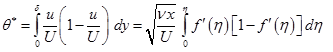(5.9.17) |
This integration is carried out numerically from 
to any arbitrary point 
and the results give rise to the following relation;
 |
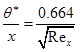(5.9.18) |
Comparing the Eqs (5.9.13, 5.9.16 & 5.9.18), it is seen that the all are inversely proportional to the square root of Reynolds number except the difference in magnitude. The value of 
is about 34% of 
while 
turns out to be approximately 13% of at any x -location (Fig. 5.9.3).
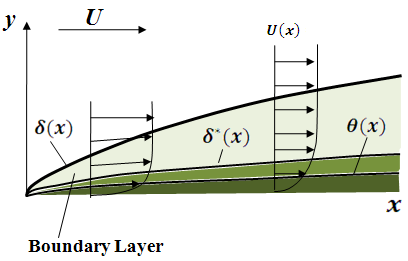
Fig. 5.9.3: Boundary layer thickness, displacement thickness and momentum thickness for a flat plate.