No analytical solution is available till date for the above boundary layer equations. However, this equation was solved first by numerically in the year 1908 by P.R.Heinrich Blasius and commonly known as Blasius solution for laminar boundary layer over a flat plate . The key for the solution is the assumption of similarity which means there is no characteristics length scale in the geometry of the problem. Physically, it is the case for the same flow patterns for an infinitely long flat plate regardless of any close-up view (Fig. 5.9.1-b). So, mathematically a similarity variable can be defined that combines the independent variables x and y into a non-dimensional independent variable. In accordance with the similarity law, the velocity profile is represented in the functional form;

(5.9.3)

With the order of magnitude analysis, the thickness of the boundary layer is interpreted as . Based on this analogy, Blasius set the non-dimensional similarity variable in the following functional form;

(5.9.4)

Now, let us introduce the stream function for the two-dimensional flow.

(5.9.5)

The stream function can be obtained through integration of Eq. (5.9.5) and using the results of Eqs (5.9.3 & 5.9.4).

(5.9.6)

Again, differentiate Eq. (5.9.6) with respect to y and use Eq. (5.9.4) to obtain the x -component of velocity profile within the boundary layer as function (Fig. 5.9.2).

(5.9.7)

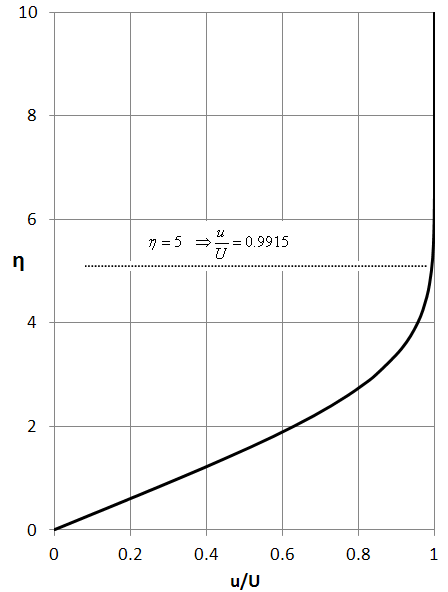
Fig. 5.9.2: Blasius profile for a laminar boundary layer over a flat plate.