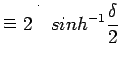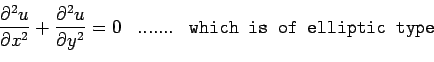: Derivation of an exact
: Difference Notation
: Difference operators
In order to obtain formulas for numerical differentiation, by
operational methods, it is necessary to relate D (the differential
operator) to the operators
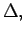
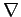
and
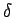
(delta
operators). For this purpose, we notice that the familiar formula
of the Taylor-series expansion
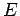 and
and
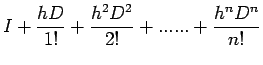 are equivalent when applied to any polynomial
are equivalent when applied to any polynomial
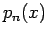 of
degree
of
degree 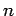 for any n.
for any n.
Further, we obtain the additional relations
Classification of second order PDES':
The
general linear second order partial differential equation in two
independent variables is given by
where the coefficients are functions of x and y and the subscripts
denote partial derivatives with respect to the independent
variables. The above equation is called
This classification depends in general on the region of the
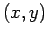
plane under consideration. The differential equation
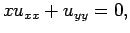
for instance, is elliptic for
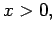
Heat Flow equation:
Wave equation:
Laplace equation:
The parabolic and hyperbolic type of equations are either initial value problems or initial boundary value problems whereas the elliptic type equation is always a boundary value problem. The boundary conditions can be one of the following three types:
- The Disichlet or first boundary condition: Here,
the solution is prescribed along the boundary
- The Neumann or Second boundary condition: Here,
the derivative of the solution is specified along the boundary.
- The third a mixed boundary condition:
Here, the solution and its derivative are prescribed along the
boundary.



: Derivation of an exact
: Difference Notation
: Difference operators
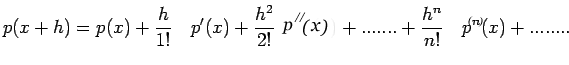
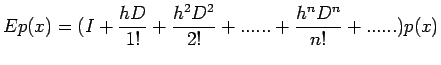
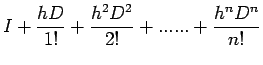 are equivalent when applied to any polynomial
are equivalent when applied to any polynomial
![$\displaystyle = 2\quad
log\left[\left(I+\frac{1}{4}\delta^{2}\right)^{\frac{1}{2}}+\frac{1}{2}\delta\right]$](img83.png)