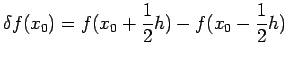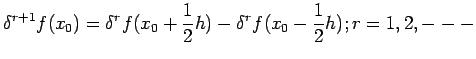: Difference operators
: lect2
: lect2
It is conventional to define the forward
difference
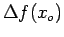 as
as
If also
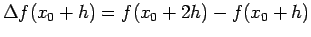 is known, then
the second forward difference associated with the point
is known, then
the second forward difference associated with the point 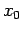 is
defined as
is
defined as
and succeeding forward differences are defined by iteration. More
generally, we introduce the definitions
where h is the spacing.
We now define the backward difference
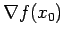 as
and higher order backward
differences are defined by iteration as
as
and higher order backward
differences are defined by iteration as
We also define Central difference
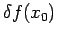 as
as
and higher order central differences
>From these definition, one can also observe



: Difference operators
: lect2
: lect2
root
平成18年1月31日
![]() as
as