


Next:Elliptic equations Up:Main
Previous:Convergence:
Hyperbolic Equation in one space variable:
The simplest hyperbolic problem is that of the vibrating string
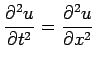 |
(24) |
in the domain
![$ R=[0\leq x\leq 1]\times[t>0],$](img247.png) satisfying the following initial conditions
satisfying the following initial conditions
and boundary conditions
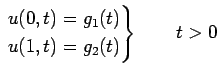 |
(26) |
We place a mesh of points
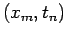 on R, where
on R, where
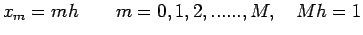
The exact difference replacement of (24) at the nodal points
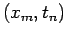 is given by
is given by
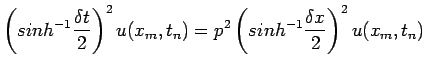 |
(27) |
where 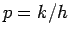 is mesh ratio and
The explicit and implicit difference scheme for (24) will be obtained by approximating equation (27).
is mesh ratio and
The explicit and implicit difference scheme for (24) will be obtained by approximating equation (27).
Explicit Difference Schemes:
An explicit difference scheme for (24) is given by
which may be written in the form
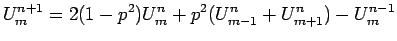 |
(28) |
where 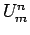 is the approximation to
is the approximation to
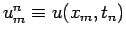 .
.
If each term in (28) is expanded in Taylor's series about the nodal point
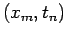 and the function
and the function
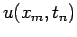 satisfies (24), then we get the truncation error
For p=1, the truncation error vanishes and so the difference representation of (24) is obtained as
In order to start computation, we require data on the two lines
satisfies (24), then we get the truncation error
For p=1, the truncation error vanishes and so the difference representation of (24) is obtained as
In order to start computation, we require data on the two lines 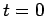 and
and 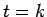 . The first condition in (25) gives
. The first condition in (25) gives 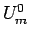 on the initial line as
We can use the second condition in (25) to find values on the line
on the initial line as
We can use the second condition in (25) to find values on the line 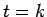 . Using the central difference approximation for the derivative, i.e
In the second condition in (25) and eliminating
. Using the central difference approximation for the derivative, i.e
In the second condition in (25) and eliminating
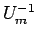 from (28) for n=0, we get the formula to give the values on the first time level,
The boundary conditions (26) become
from (28) for n=0, we get the formula to give the values on the first time level,
The boundary conditions (26) become
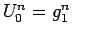 and
and
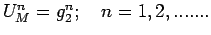
Formula (27) may now be used to advance computation for 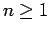 .
.
To examine the finite difference formula (27) for stability, we replace 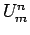 by
by
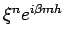 and get
or
and get
or
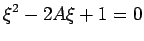 |
(29) |
where
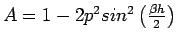
The solution of (29) is given by
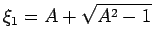
and
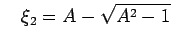
This gives that
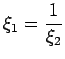 .
Thus for stability
.
Thus for stability
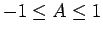 or
or
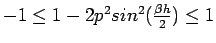 , which gives
, which gives 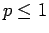 .
.
This is the condition of stability.
Implicit Difference Scheme:
In order to improve stability, we now consider an implicit difference replacement of equation (25). This takes the form
where 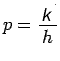 . One can examine this scheme for stability and find that the scheme is stable for all
. One can examine this scheme for stability and find that the scheme is stable for all 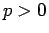 if
if
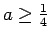 . Thus, if
. Thus, if
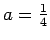 , the implicit difference formula
, the implicit difference formula
The consistency of a finite difference approximation to a hyperbolic equation can be defined briefly. A difference scheme to a hyperbolic equation is consistent; if
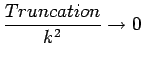 as
as
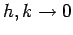 .
.


Next:Elliptic equations:Up:Main
Previous:Convergence:

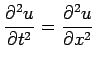
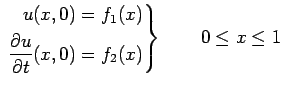
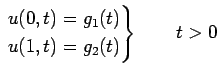
![]() on R, where
on R, where
![]()
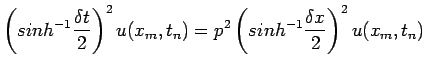
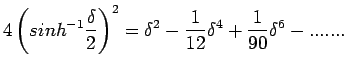
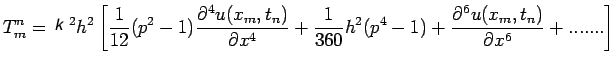
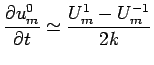
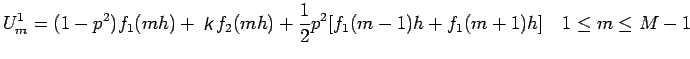
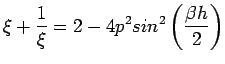
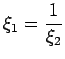 .
.
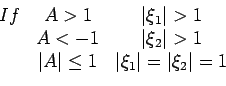
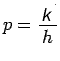 . One can examine this scheme for stability and find that the scheme is stable for all
. One can examine this scheme for stability and find that the scheme is stable for all ![$\displaystyle =\frac{4}{p^{2}}\left[U^{n+1}_{m}-2U^{n}_{m}+U^{n-1}_{m}\right]$](img289.png)
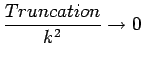 as
as
![]() .
.