


Next:Convergence:Up:Main
Previous:Explicit Formulae
Solution of Tridiagonal systems:
The implicit difference formula given above has involved three unknown values of U at the advanced time level 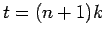 . The system of linear algebraic equations arising from the implicit difference formulae which must be solved at each time step is a special case of the tridiagonal system
. The system of linear algebraic equations arising from the implicit difference formulae which must be solved at each time step is a special case of the tridiagonal system
for
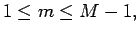 where
where 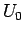 and
and 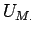 are known from the boundary condition. If
are known from the boundary condition. If
and
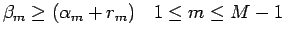 , a highly efficient method is known for solving the tridiagonal system. The method is given as follows:
, a highly efficient method is known for solving the tridiagonal system. The method is given as follows:
consider the difference relation
for
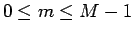 , from which it follows that
If this is used to eliminate
, from which it follows that
If this is used to eliminate 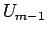 from the original difference formula defining the tridiagonal system, the result
is obtained, and so
If
from the original difference formula defining the tridiagonal system, the result
is obtained, and so
If 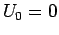 , then
, then
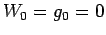 , in order that the difference relation
holds for any
, in order that the difference relation
holds for any 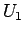 . The remaining
. The remaining
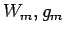
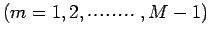 can now be computed as
can now be computed as
.
.
.
.
.
.
.
If 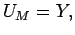 then
then
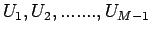 are computed as
are computed as
.
.
.
.
.
.
.
In using this method, substantial errors will appear in the computed values of

unless
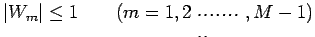
Now
and so on, since
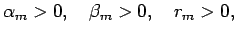
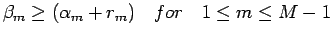 . This leads to
. This leads to
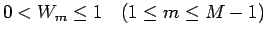 .
.


Next:Convergence:Up:Main
Previous:Explicit Formulae

![]() . The system of linear algebraic equations arising from the implicit difference formulae which must be solved at each time step is a special case of the tridiagonal system
. The system of linear algebraic equations arising from the implicit difference formulae which must be solved at each time step is a special case of the tridiagonal system
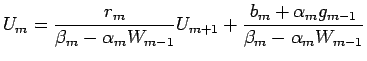
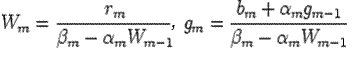
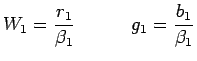
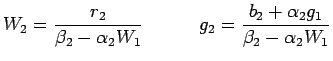
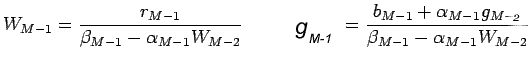
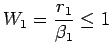
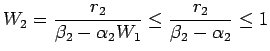
![]()
![]() . This leads to
. This leads to
![]() .
.