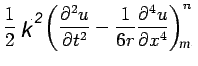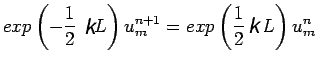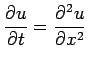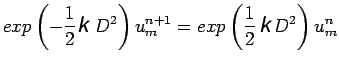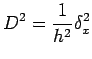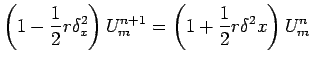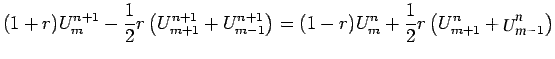Next:Solution of Tridiagonal systems: Up:Main Previous:Derivation of an exact difference formula
Explicit Formulae
An explicit formula involves only one grid point at the advanced time level
t=(n+1)k
Consider the heat equation given by
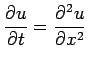 |
(5) |
Here 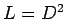 and equation(2) becomes
and equation(2) becomes
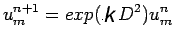 |
(6) |
and from equation (3), we have
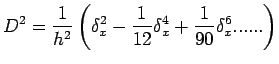 |
(7) |
Substituting this value of 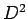 in equation (6) followed by expansion leads to
in equation (6) followed by expansion leads to
![$\displaystyle u^{n+1}_{m}=\left[1+r\delta^{2}_{x} + \frac{1}{2}r\left(r-\frac{1}{6}\right)\delta^{4}_{x} + ...... \right]u^{n}_{m }$](img116.png) |
(8) |
where
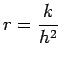 is the mesh ratio. From equation (8), if we retain only second order central differences, the forward difference formula
is the mesh ratio. From equation (8), if we retain only second order central differences, the forward difference formula
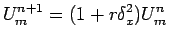 |
(9) |
is obtained which, on substitution for
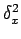 leads to
leads to
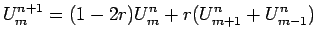 |
(10) |
where 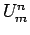 is an approximation to
is an approximation to
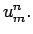
Truncation Error:
Let us investigate the local accuracy of the finite difference formula(10). Introduce the difference between the exact solution of the differential and difference equations at the grid point 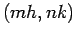 as
as
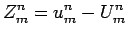 |
(11) |
Using Taylor's theorem
and so
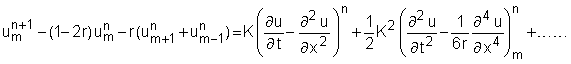 (12)
(12)
>From equation (5), (10), (11) and (12), the result
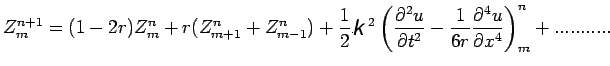 is obtained. The quantity
is obtained. The quantity
 |
(13) |
is defined as the local truncation error of formula (10) and the principal part of the truncation error is
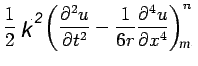 |
(14) |
Implicit Formulae:
An implicit formula involves more than one grid point at the advanced time level 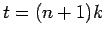 . These formulae can often be obtained from equation (2) written in the central form
. These formulae can often be obtained from equation (2) written in the central form
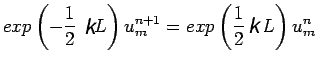 |
(15) |
For the heat equation
the equation (15) becomes
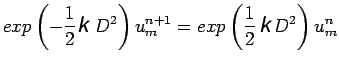 |
(16) |
correct to second differences
and substitution in equation (16) followed by expansion leads to the central difference formula
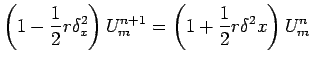 |
(17) |
with a principal truncation error of
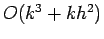 . This is the Crank-Nicolson formula and may be written in the form
. This is the Crank-Nicolson formula and may be written in the form

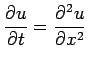
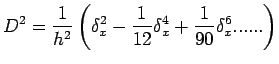
![$\displaystyle u^{n+1}_{m}=\left[1+r\delta^{2}_{x} + \frac{1}{2}r\left(r-\frac{1}{6}\right)\delta^{4}_{x} + ...... \right]u^{n}_{m }$](img116.png)
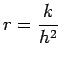 is the mesh ratio. From equation (8), if we retain only second order central differences, the forward difference formula
is the mesh ratio. From equation (8), if we retain only second order central differences, the forward difference formula
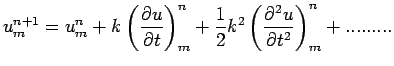
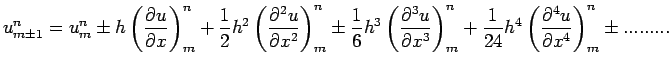
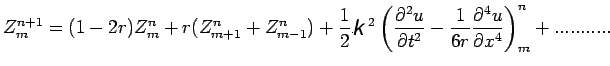 is obtained. The quantity
is obtained. The quantity