


Next: Differentiation Formulas Up:Main Previous: Difference Notation
For many purposes, it is convenient to think of the symbols
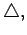
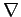
and
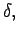
defined earlier, as operators,
which transform a given function
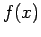
into related functions,
according to the laws:
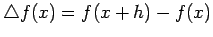
In addition, we also define the following:
Averaging operator , denoted by 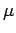 and
defined as
Shift operator, denoted by
and
defined as
Shift operator, denoted by 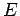 , and defined as
, and defined as
and the differential operator, denoted by 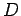 and defined as
and defined as
In all these operators except D, the spacing h is implied.
Positive integral powers of these operators are defined by
iteration. Also we define the zeroeth power of any operator as the
identity operator I, which leaves any function
unchanged. For the operator
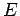
, the power
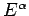
is defined
for any
real 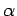
so that
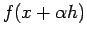 . In view of the above,
we also have
. In view of the above,
we also have
so that
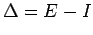
Again
giving
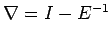
Also
and thus
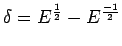
Moreover,
and thus
Hence the operators 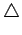 ,
, 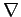 ,
, 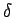 and
and 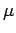 , are
simply expressed in terms of
, are
simply expressed in terms of 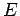 . From the above relations, we may
deduce the relations
after which the formal symbolism of elementary algebra suggests
the forms
and
. From the above relations, we may
deduce the relations
after which the formal symbolism of elementary algebra suggests
the forms
and
while the
first form requires no explanation, the form
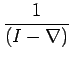
can be interpreted at this stage only as
representing the inverse of operator
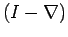
, that is, as an
alternative notation of the operator
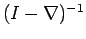
such that
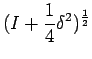 is to represent an
operator such that its iterate is the
operator
is to represent an
operator such that its iterate is the
operator
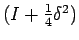 ,
,
![$ \left[\left(I+\frac{1}{4}\delta^{2}\right)^{\frac{1}{2}}\right]^{2}=I+\frac{1}{4}\delta^{2}$](img72.png)


Next:Differentiation Formulas
Up:Main Previous: Difference Notation

![]()
![]()
![]()
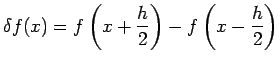
![$\displaystyle \mu
f(x)=\frac{1}{2}\left[f\left(x+\frac{h}{2}\right)+f\left(x-\frac{h}{2}\right)\right]$](img28.png)
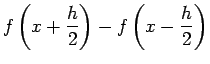
![$\displaystyle \frac{1}{2}\left[f\left(x+\frac{h}{2}\right)+f\left(x-\frac{h}{2}\right)\right]$](img53.png)
![$\displaystyle \frac{1}{2}\left[E^{\frac{1}{2}}f(x)+E^{\frac{-1}{2}}f(x)\right]$](img54.png)
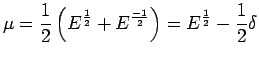
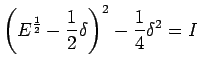
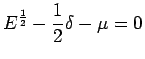
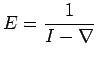
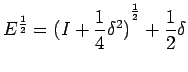
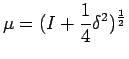
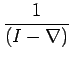 can be interpreted at this stage only as
representing the inverse of operator
can be interpreted at this stage only as
representing the inverse of operator
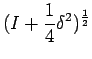 is to represent an
operator such that its iterate is the
operator
is to represent an
operator such that its iterate is the
operator
![$ \left[\left(I+\frac{1}{4}\delta^{2}\right)^{\frac{1}{2}}\right]^{2}=I+\frac{1}{4}\delta^{2}$](img72.png)