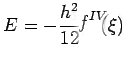: Numerical Integration:
: lec1
: Gaussian Elimination
The basic idea behind numerical
differentiation is very simple. If given the set of values
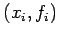 i=0,1,...,n, we determine the interpolating polynomial
i=0,1,...,n, we determine the interpolating polynomial
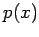 through these points. We then differentiate this polynomial
to obtain
through these points. We then differentiate this polynomial
to obtain 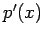 whose values for any
whose values for any 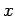 is taken as an
approximation to
is taken as an
approximation to 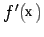 . Let us very briefly describe this
interpolating polynomial.
. Let us very briefly describe this
interpolating polynomial.
Let
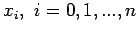 be
be 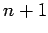 distinct points on an interval
I and let
distinct points on an interval
I and let 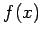 be a real valued function which takes on the
values
be a real valued function which takes on the
values
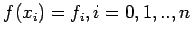 , at these n+1 points. To construct
a polynomial of degree not exceeding n which passes through the
n+1 points
, at these n+1 points. To construct
a polynomial of degree not exceeding n which passes through the
n+1 points
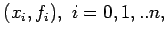 we use the method of
Lagrange. We begin by expressing the desired polynomial as
where each
we use the method of
Lagrange. We begin by expressing the desired polynomial as
where each
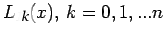 is a polynomial of degree not
exceeding n. The interpolation condition
is a polynomial of degree not
exceeding n. The interpolation condition
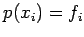 will be
satisfied if the
will be
satisfied if the  satisfy:
It is easy to verify that the function defined by
have this property.
satisfy:
It is easy to verify that the function defined by
have this property.
The error in approximating 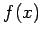 by such a polynomial
by such a polynomial 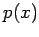 is
given by
where and
is
given by
where and
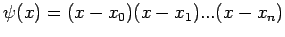 and
and 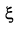 is some
point on the interval containing
is some
point on the interval containing
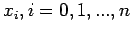 Then the error
in the derivative
Then the error
in the derivative 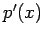 at a tabular point
at a tabular point 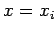 is given by
Where
is given by
Where 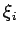 is a point in the interval containing the points
is a point in the interval containing the points
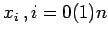 and
If we assume that the interpolating points
and
If we assume that the interpolating points
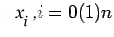 are
equally spaced with spacing h, and put
are
equally spaced with spacing h, and put
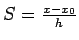 we can
approximate
we can
approximate 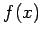 by Newton's forward difference formula given by
Where
by Newton's forward difference formula given by
Where 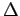 is the forward difference
operation definition
and
is the forward difference
operation definition
and
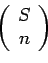 is the binomial coefficient given by
The error is
is the binomial coefficient given by
The error is
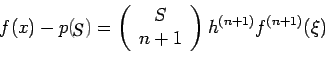 .
.
Differentiating (1) w. r. h. x and noting that
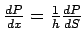
We obtain
If we now set
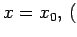 ie
ie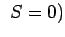 we obtain Approximation formulas for
we obtain Approximation formulas for 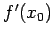 for different
values of n. For example, for
for different
values of n. For example, for 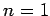 , we have
with the error of this formula given by
Taking now n=2,
with the error given by
Formulas for approximation higher derivation of
, we have
with the error of this formula given by
Taking now n=2,
with the error given by
Formulas for approximation higher derivation of 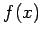 can be
obtained in a similar manner. Differentiating (1) twice and
setting
can be
obtained in a similar manner. Differentiating (1) twice and
setting 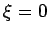 , we obtain
with the error given by
, we obtain
with the error given by
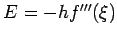
Another formula for the derivatives, using central difference, is
given by
where
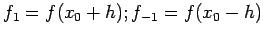
Using Taylor's expansion about the  , we get
This gives
If
, we get
This gives
If 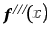 is continuous on
is continuous on
![$ [x_{-1},x_1]$](img486.png) , we have
as thus the error in the formula is
The simplest formula
, we have
as thus the error in the formula is
The simplest formula
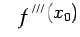 based on central difference is
based on central difference is
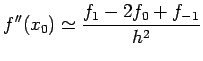
with error
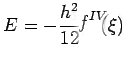



: Numerical Integration:
: lec1
: Gaussian Elimination
root
平成18年1月24日
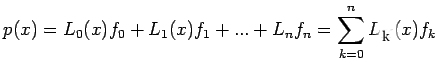
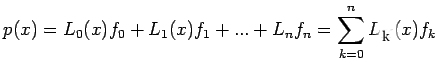
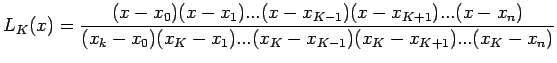
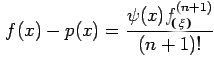
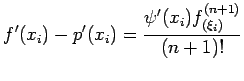
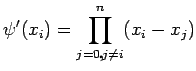
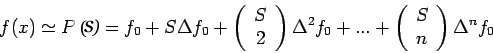
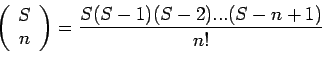
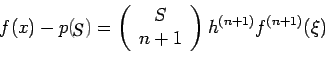 .
.
![\begin{displaymath}f'(x)\simeq\frac{1}{h}\frac{dP}{dS}=\frac{1}{h}[\Delta f_0+\f...
...in{array}{c}
S \\
n \\
\end{array}%
\right)\Delta^nf_0]\end{displaymath}](img467.png)
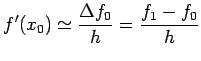
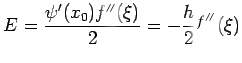
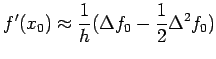
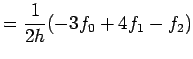
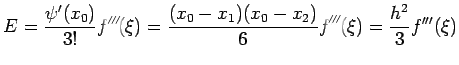
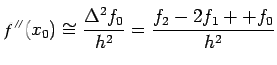
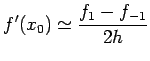
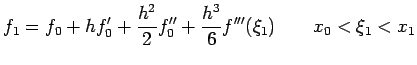
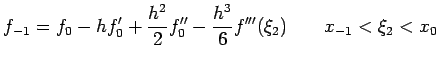
![$\displaystyle \frac{f_1-f_{-1}}{2h}=f'(x_0)+\frac{h^2}{12}[f'''(\xi_1)+f'''(\xi_2)]$](img484.png)
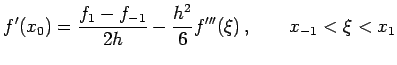
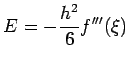
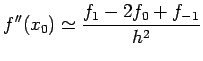 with error
with error