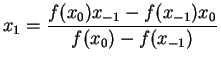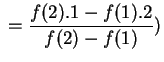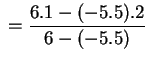Next: Convergence of secant method:
Up: (b)False position or Regula
Previous: (b)False position or Regula
In this method an improvement over Regular Falsi method is
obtained by replacing the secant by straight lines of even-smaller
slope until 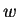 falls to the otherside of the zero of
falls to the otherside of the zero of 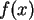 . The
various steps in the method are given in the algorithm below:
. The
various steps in the method are given in the algorithm below:
Algorithm:
Given a function 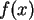 continuous on an
interval
continuous on an
interval ![$ [a,b]$](img37.png) satisfying the criteria
satisfying the criteria
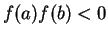 , carry out
the following steps to find the root of
, carry out
the following steps to find the root of 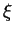 of
of 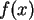 in
in
![$ [a,b]$](img37.png) :
:
(1) Set
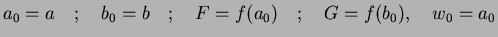
(2) For n=0,1,2...., until convergence criteria is satisfied,
do:
(a) compute
![$ w_{n+1}=[Ga_{n}-Fb_{n}]/(G-F)$](img106.png)
(b) If
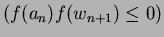 then
then
Set
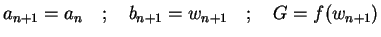
Also if
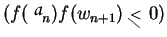 Set
Set 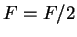
Otherwise
Set
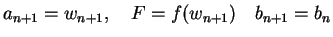
Also if
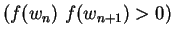 Set
Set 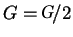
Example:
Solve
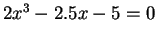 for the root in the
interval [1,2] by modified Regula Falsi method.
for the root in the
interval [1,2] by modified Regula Falsi method.
Solution: Since
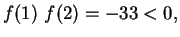 we go ahead with
finding the root of given function f(x) in [1,2]. Setting
we go ahead with
finding the root of given function f(x) in [1,2]. Setting
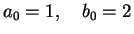 and following the above algorithm. Result
are provided in
the table below:
and following the above algorithm. Result
are provided in
the table below:
| |
|
Modified Regula Falsi Method |
|
|
|---|
| Iteration no. |
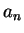 |
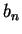 |
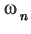 |
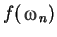 |
| 0 |
1.0000000000 |
2.0000000000 |
1.4782608747 |
-2.2348976135 |
| 1 |
1.4782608747 |
2.0000000000 |
1.7010031939 |
0.5908976793 |
| 2 |
1.4782608747 |
1.7010031939 |
1.6544258595 |
-0.0793241411 |
| 3 |
1.6544258595 |
1.7010031939 |
1.6599385738 |
-0.0022699926 |
| 4 |
1.6599385738 |
1.7010031939 |
1.6602516174 |
0.0021237291 |
| 5 |
1.6599385738 |
1.6602516174 |
1.6601003408 |
0.0000002435 |
The geometric view of the example is provided in the figure
below:
Example:
Solve
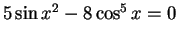 for the root in the
interval [0.5,1.5] by modified Regula Falsi method.
for the root in the
interval [0.5,1.5] by modified Regula Falsi method.
| |
|
Modified Regula Falsi Method |
|
|
|---|
| Iteration no. |
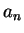 |
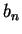 |
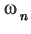 |
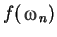 |
| 0 |
0.5000000000 |
1.5000000000 |
0.8773435354 |
2.1035263538 |
| 1 |
0.5000000000 |
0.8773435354 |
0.7222673893 |
0.2828366458 |
| 2 |
0.5000000000 |
0.7222673893 |
0.6871531010 |
-0.1967970580 |
| 3 |
0.6871531010 |
0.7222673893 |
0.7015607357 |
0.0026464546 |
| 4 |
0.6871531010 |
0.7015607357 |
0.7013695836 |
0.0000239155 |
| 5 |
0.6871531010 |
0.7013695836 |
0.7013661265 |
-0.0000235377 |
| 6 |
0.7013661265 |
0.7013695836 |
0.7013678551 |
-0.0000003363 |
Secant Method: Like the Regula Falsi method and the
Bisection method this method also requires two initial estimates
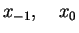 of the root of f(x)=0 but unlike those
earlier methods it gives up the demand of bracketing the root.
Like in the Regular Falsi method, this method too retains the use
of secants throughout while tracking the root of f(x)=0. The
secant joining the points
of the root of f(x)=0 but unlike those
earlier methods it gives up the demand of bracketing the root.
Like in the Regular Falsi method, this method too retains the use
of secants throughout while tracking the root of f(x)=0. The
secant joining the points
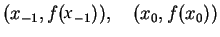 is given by
is given by
Say it intersects with x-axis at 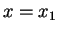 , then
If
, then
If
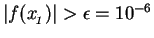 (say) then replace
(say) then replace
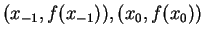 with
with
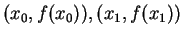 and repeat the process to get
and repeat the process to get 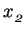 and so on . The
method is algorithmically described
below:
and so on . The
method is algorithmically described
below:
Algorithm:
Given a 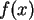 , two initial points a, b and
, two initial points a, b and
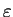 the required level of accuracy carry out the
following steps to find the root
the required level of accuracy carry out the
following steps to find the root 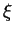 of f(x)=0.
of f(x)=0.
(1) Set
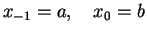
(2) For n=0,1,2... until convergence criteria is satisfied, do:
Compute
Example:
Solve
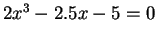 for the root with
for the root with
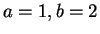 by secant method to an accuracy of
by secant method to an accuracy of 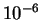 .
.
Solution:
Set
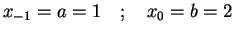
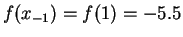
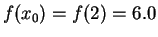
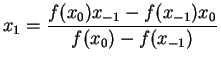
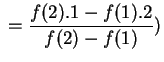
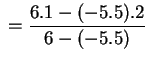
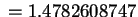
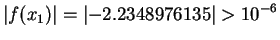
 Repeat the
process with
Repeat the
process with
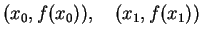 and so on
till you get a
and so on
till you get a 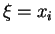 s.t.
s.t.
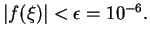 These
results are tabulated below:
These
results are tabulated below:
| |
|
Secant Method |
|
|
|---|
| |
|
|
|
|
| Iteration no. |
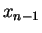 |
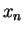 |
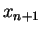 |
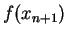 |
| 0 |
1.0000000000 |
2.0000000000 |
1.4782608747 |
-2.2348976135 |
| 1 |
2.0000000000 |
1.4782608747 |
1.6198574305 |
-0.5488323569 |
| 2 |
1.4782608747 |
1.6198574305 |
1.6659486294 |
0.0824255496 |
| 3 |
1.6198574305 |
1.6659486294 |
1.6599303484 |
-0.0023854144 |
| 4 |
1.6659486294 |
1.6599303484 |
1.6600996256 |
-0.0000097955 |
Geometrical Visualization of the root tracking procedure by secant
method for the above example:



Next: Convergence of secant method:
Up: (b)False position or Regula
Previous: (b)False position or Regula
root
2006-02-07
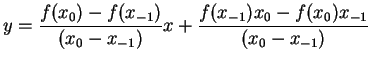
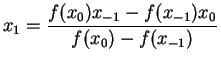
![$\displaystyle x_{n+1}=\frac{[f(x_{n})x_{n-1}-f(x_{n-1})x_{n}]}{[f(x_{n})-f(x_{n-1})]}$](img127.png)