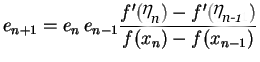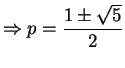Next: Newton-Raphson Method:
Up: ratish-1
Previous: Modified Regular Falsi method:
Definition: Say,
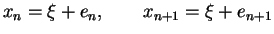 where
where 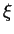 is the root of
is the root of 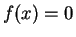 .
. 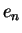 ,
, 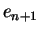 are the errors at n
are the errors at n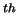 and (n+1)
and (n+1)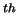 iterations and
iterations and
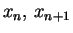 are the approximations of
are the approximations of 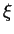 at
at 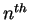 ,
(n+1)
,
(n+1)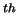 , iterations. If
, iterations. If
 where
where  is
a constant, then the rate of convergence of the method by which
is
a constant, then the rate of convergence of the method by which
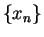 is generated is p.
is generated is p.
Claim: Secant method has super linear convergence.
Proof: The iteration scheme for the secant method is
given by
Say 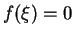 and
and
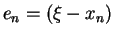 i.e the error in the
n
i.e the error in the
n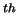 iteration in estimating
iteration in estimating 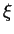 .
.
Using (iii) in (ii) we get
By Mean value Theorem,
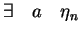 in the
interval
in the
interval 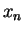 and
and 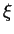 s.t.
We get
s.t.
We get
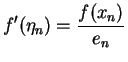
i.e.
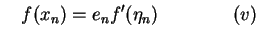
Using (iii)above, we get
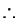 using (v), (vi), in (iv) we get
By def of rate of convergence the method is of order p if
>From (vii) and (viii) we get
using (v), (vi), in (iv) we get
By def of rate of convergence the method is of order p if
>From (vii) and (viii) we get
i.e.
i.e.
From
(viii), (ix) we get
i.e.
Hence the convergence is superlinear.
Example:
Solve
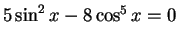 for the root
in the interval [0.5,1.5] by secant method.
for the root
in the interval [0.5,1.5] by secant method.
| |
|
Secant Method |
|
|
|---|
| |
|
|
|
|
| 0 |
0.5000000000 |
1.5000000000 |
0.8773435354 |
2.1035263538 |
| 1 |
1.5000000000 |
0.8773435354 |
0.4212051630 |
-4.2280626297 |
| 2 |
0.8773435354 |
0.4212051630 |
0.7258019447 |
0.3298732340 |
| 3 |
0.4212051630 |
0.7258019447 |
0.7037572265 |
0.0327354670 |
| 4 |
0.7258019447 |
0.7037572265 |
0.7013285756 |
-0.0005388701 |
| 5 |
0.7037572265 |
0.7013285756 |
0.7013679147 |
0.0000009526 |



Next: Newton-Raphson Method:
Up: ratish-1
Previous: Modified Regular Falsi method:
root
2006-02-07
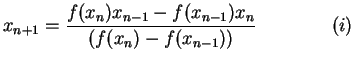
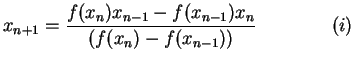
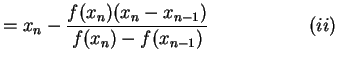
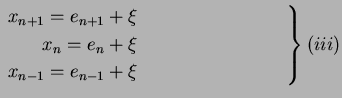
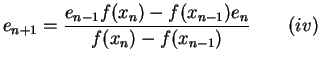
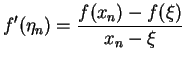
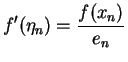 i.e.
i.e.