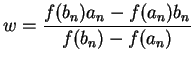Next: Modified Regular Falsi method:
Up: ratish-1
Previous: Bracketing Methods:
Bisection method converges slowly. Here while defining the new
interval
![$ [a_{n}, b_{n}]$](img50.png) the only utilization of the function
the only utilization of the function
 is in checking whether
is in checking whether
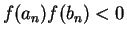 but not in
actually calculating the end point of the interval. False position
or Regular Falsi method uses
but not in
actually calculating the end point of the interval. False position
or Regular Falsi method uses  not only in deciding the new
interval
not only in deciding the new
interval
![$ [a_{n}, b_{n}]$](img50.png) as in bisection method but also in
calculating one of the end points of the new interval. Here one of
end points of
as in bisection method but also in
calculating one of the end points of the new interval. Here one of
end points of
![$ [a_{n}, b_{n}]$](img50.png) say
say 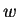 is calculated as a weighted
average defined on previous interval
is calculated as a weighted
average defined on previous interval
![$ [a_{n-1},\quad b_{n-1}]$](img84.png) as:
as:
(
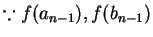 have opposite signs).
have opposite signs).
The algorithm for computing the root of function  by thus
method is given below.
by thus
method is given below.
Algorithm:
Given a  continuous on an interval
continuous on an interval ![$ [a,b]$](img37.png) satisfying the
criteria
satisfying the
criteria
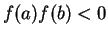 , carry out the
following steps to find the root
, carry out the
following steps to find the root 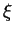 of
of  in
in ![$ [a,b]$](img37.png) :
:
(1) Set
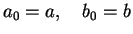
(2) For n = 0,1,2.... until convergence criteria is satisfied
do:
(a) Compute
![$ \displaystyle {w=\frac{[f(b_{n})a_{n}-f(a_{n})b_{n}]}{[{f(b_{n})-f(a_{n})}]}} $](img88.png)
(b) If
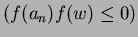 Then
Then
set
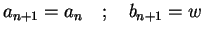
otherwise
set
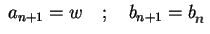
Note:
Use any one of the convergence criteria discussed earlier under
bisection method. For the sake of carrying out a comparative we
will stick both to the same convergence criteria as before i.e.
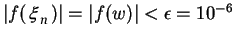 (say)
and to the example problems.
(say)
and to the example problems.
Example:
Solve
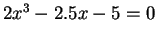 for the root in the
interval [1,2] by Regula-Falsi method:
for the root in the
interval [1,2] by Regula-Falsi method:
Solution: Since
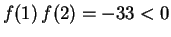 , we go ahead in
finding the root of given function f(x) in [1,2].
, we go ahead in
finding the root of given function f(x) in [1,2].
Set
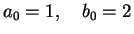 .
.
set
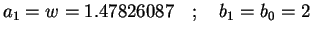
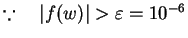 proceed with
iteration.
proceed with
iteration.
Iteration details are provide below in a tabular form:
| |
|
Regula Falsi Method |
|
|
|---|
| |
|
|
|
|
| Iteration no. |
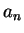 |
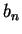 |
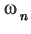 |
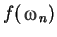 |
| 0 |
1.0000000000 |
2.0000000000 |
1.4782608747 |
-2.2348976135 |
| 1 |
1.4782608747 |
2.0000000000 |
1.6198574305 |
-0.5488323569 |
| 2 |
1.6198574305 |
2.0000000000 |
1.6517157555 |
-0.1169833690 |
| 3 |
1.6517157555 |
2.0000000000 |
1.6583764553 |
-0.0241659321 |
| 4 |
1.6583764553 |
2.0000000000 |
1.6597468853 |
-0.0049594725 |
| 5 |
1.6597468853 |
2.0000000000 |
1.6600278616 |
-0.0010169938 |
| 6 |
1.6600278616 |
2.0000000000 |
1.6600854397 |
-0.0002089010 |
| 7 |
1.6600854397 |
2.0000000000 |
1.6600972414 |
-0.0000432589 |
| 8 |
1.6600972414 |
2.0000000000 |
1.6600997448 |
-0.0000081223 |
Note : One may note that Regular Falsi method has
converged faster
than the Bisection method.
Geometric Interpretation of Regula Falsi Method:
Let us plot the polynomial considered in the above example and
trace 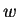 , its movement and new intervals
, its movement and new intervals
![$ [a_{n}, b_{n}]$](img50.png) with
iteration. From the figure() one can verify that the weighted
average
is the point of intersection of the secant to
with
iteration. From the figure() one can verify that the weighted
average
is the point of intersection of the secant to 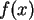 , passing
through points
, passing
through points
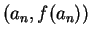 and
and
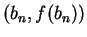 with the
x-axis. Since here
with the
x-axis. Since here 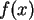 is concave upward and increasing the
secant is always above
is concave upward and increasing the
secant is always above 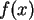 . Hence,
. Hence, 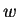 always lies to the left
of the zero. If
always lies to the left
of the zero. If 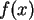 were to be concave downward and increasing,
were to be concave downward and increasing,
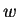 would always lie to the right of the zero.
would always lie to the right of the zero.
Example:
Solve
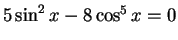 for the root
in the interval [0.5,1.5] by Regular Falsi method.
for the root
in the interval [0.5,1.5] by Regular Falsi method.
| |
|
Regula Falsi Method |
|
|
|---|
| |
|
|
|
|
| Iteration no. |
 |
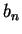 |
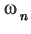 |
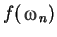 |
| 0 |
0.5000000000 |
1.5000000000 |
0.8773435354 |
2.1035263538 |
| 1 |
0.5000000000 |
0.8773435354 |
0.7222673893 |
0.2828366458 |
| 2 |
0.5000000000 |
0.7222673893 |
0.7032044530 |
0.0251714624 |
| 3 |
0.5000000000 |
0.7032044530 |
0.7015219927 |
0.0021148270 |
| 4 |
0.5000000000 |
0.7015219927 |
0.7013807297 |
0.0001767781 |
| 5 |
0.5000000000 |
0.7013807297 |
0.7013689280 |
0.0000148928 |
| 6 |
0.5000000000 |
0.7013689280 |
0.7013679147 |
0.0000009526 |
Subsections



Next: Modified Regular Falsi method:
Up: ratish-1
Previous: Bracketing Methods:
root
2006-02-07
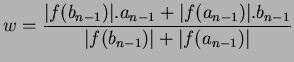
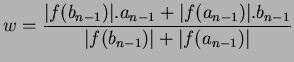
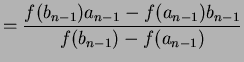
![$ \displaystyle {w=\frac{[f(b_{n})a_{n}-f(a_{n})b_{n}]}{[{f(b_{n})-f(a_{n})}]}} $](img88.png)