Next: Modified Regular Falsi method: Up: MAIN Previous: Bracketing Methods:

False Position or Regula Falsi method:

Bisection method converges slowly. Here while defining the new interval $[a_{n}, b_{n}]$ the only utilization of the function $'f(x)'$ is in checking whether $f(a_{n})f(b_{n})<0$ but not in actually calculating the end point of the interval. False Position or Regular Falsi method uses not only in deciding the new interval $[a_{n}, b_{n}]$ as in bisection method but also in calculating one of the end points of the new interval. Here one of end points of $[a_{n}, b_{n}]$ say $w$ is calculated as a weighted average defined on previous interval as

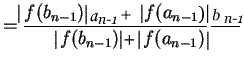
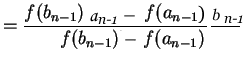
( $\because f(a_{n-1}),f(b_{n-1})$ have opposite signs).
The algorithm for computing the root of function by this method is given below.
Algorithm:
Given a function continuous on an interval $[a,b]$ satisfying the criteria $f(a)f(b)<0$, carry out the following steps to find the root $\xi$ of in $[a,b]$:
(1) Set $a_{0}=a,\quad b_{0}=b$
(2) For n = 0,1,2.... until convergence criteria is satisfied , do:
(a) Compute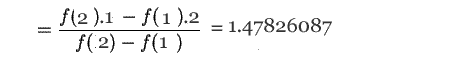     

(b) If  ,   then set $a_{n+1}=a_{n}\quad ;\quad b_{n+1}=w$
otherwise set
Note:
Use any one of the convergence criteria discussed earlier under bisection method. For the sake of carrying out a comparative study we will stick both to the same convergence criteria as before i.e. (say) and to the example problems.
Example:
Solve $2x^{3}-2.5x-5=0$ for the root in the interval [1,2] by Regula-Falsi method:

Solution: Since $f(1)\, f(2)=-33<0$, we go ahead in finding the root of given function f(x) in [1,2].
Set $a_{0}=1,\quad b_{0}=2$.

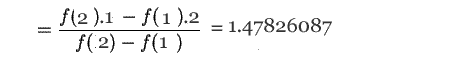
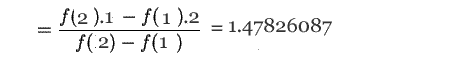
set $a_{1}=w=1.47826087\quad;\quad b_{1}=b_{0}=2$
$\because \quad \vert f(w)\vert>\varepsilon=10^{-6}$, proceed with iteration.
Iteration details are provide below in a tabular form:

		Regula Falsi Method
Iteration no.	$a_n$	$b_n$
0	1.0000000000	2.0000000000	1.4782608747	-2.2348976135
1	1.4782608747	2.0000000000	1.6198574305	-0.5488323569
2	1.6198574305	2.0000000000	1.6517157555	-0.1169833690
3	1.6517157555	2.0000000000	1.6583764553	-0.0241659321
4	1.6583764553	2.0000000000	1.6597468853	-0.0049594725
5	1.6597468853	2.0000000000	1.6600278616	-0.0010169938
6	1.6600278616	2.0000000000	1.6600854397	-0.0002089010
7	1.6600854397	2.0000000000	1.6600972414	-0.0000432589
8	1.6600972414	2.0000000000	1.6600997448	-0.0000081223

 

Note : One may note that Regula Falsi method has converged faster than the Bisection method.

Geometric Interpretation of Regula Falsi Method:

Let us plot the polynomial considered in the above example and trace $w$, its movement and new intervals $[a_{n}, b_{n}]$ with iteration. From the figure(), one can verify that the weighted average

$$w=\frac{f(b_{n})a_{n}-f(a_{n})b_{n}}{f(b_{n})-f(a_{n})}$$

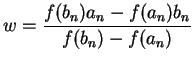
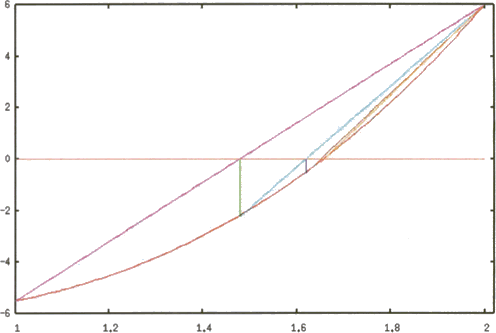
is the point of intersection of the secant to , passing through points $(a_{n},f(a_{n}))$ and $(b_{n},f(b_{n}))$ with the x-axis. Since here is concave upward and increasing the secant is always above . Hence, $w$ always lies to the left of the zero. If were to be concave downward and increasing, $w$ would always lie to the right of the zero.

 

Example:
Solve $5 \sin^{2}x-8\cos^{5}x=0$ for the root in the interval [0.5,1.5] by Regula Falsi method.

		Regula Falsi Method
Iteration no.	$a_n$	$b_n$
0	0.5000000000	1.5000000000	0.8773435354	2.1035263538
1	0.5000000000	0.8773435354	0.7222673893	0.2828366458
2	0.5000000000	0.7222673893	0.7032044530	0.0251714624
3	0.5000000000	0.7032044530	0.7015219927	0.0021148270
4	0.5000000000	0.7015219927	0.7013807297	0.0001767781
5	0.5000000000	0.7013807297	0.7013689280	0.0000148928
6	0.5000000000	0.7013689280	0.7013679147	0.0000009526

Exercise: 1) Solve for the root in the interval [2,3] by Regula-Falsi Method.

2) Find the solution to , in the interval [1,2] accurate to within using Regula-Falsi Method.