Next: False position or Regula  Up: Main  Previous: Numerical Analysis

Bracketing Methods:

(a) Bisection Method:
This is one of the simplest and reliable iterative methods for the solution of nonlinear equation. This method is also known as binary chopping or half-interval method. Given a function which is real and continuous in an interval $ [a,b]$ and $ f(a)$ and $ f(b)$ are of opposite sign i.e. $ f(a)f(b)<0$, then there is at least one real root of .

Algorithm:
Given a function continuous on a interval $ [a,b]$ satisfying the Bisection method starting criteria, carry out the following steps to find a root $ \xi$ of

(1) Set $ a_{0}=a,\quad b_{0}=b$
(2) For n=1,2,...until satisfied do

(a) If
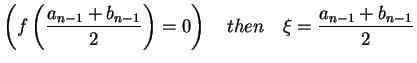
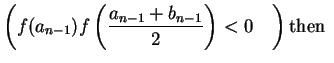
(b)If $ \displaystyle{\left(f(a_{n-1}) f\left(\frac{a_{n-1}+b_{n-1}}{2}\right)< 0\quad \right)\mbox{then }}$

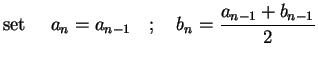
      otherwise
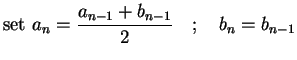
$ \displaystyle{\mbox{set } a_{n}=\frac{a_{n-1}+b_{n-1}}{2}\quad ; \quad b_{n}=b_{n-1}}$
Note:
1) The subscripts in $ a_{0},\quad b_{0},\quad a_{n-1},\quad b_{n-1},\quad a_{n},\quad b_{n}$ etc denote the iteration number. $ [a_{0}, b_{0}]$ is the interval for the zeroth or starting iteration. $ [a_{n}, b_{n}]$ is the interval for the n$ ^{th}$ iteration.

(2) An iterative process must be terminated at some stage. 'Until satisfied' refers to the solution convergence criteria used for stopping the execution process. We must have an objective criteria for deciding when to stop the process.We may use one of the following criteria depending on the behavior of the function (monotonous/steep variation/increasing /decreasing)

(i) $ \displaystyle {\vert x_{n+1}-x_{n}\vert<\epsilon_{a}}$   (Tolerable absolute error in $ \xi)$
(ii) 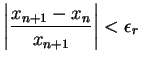  (Tolerable relative error in $ \xi)$
(iii) $ \displaystyle {\vert f(x_{n+1}\vert<\epsilon } $     (Value of function as $ x_{n}\rightarrow\xi$)
(iv) $ \vert f(x_{n+1})-f(x_{n})\vert<\epsilon$     (difference in two consecutive iteration function values)

Usually $ \epsilon_{a},\quad \epsilon_{r},\quad \epsilon$ are referred to as tolerance values and it is fixed by us depending on the level of accuracy we desire to have on the solution. For example $ \epsilon_{a}\approx 10^{-70},\quad \epsilon_{r}\approx 10^{-12},\quad \epsilon\approx10^{-10}$ etc.

Example:
Solve $ 2x^{3}-2.5x-5=0$ for the root in the interval [1,2] by Bisection method.

Solution: Given $ f(x)=2x^{3}-2.5x-5$    on $ [1,2]$
$ f(1)=-5.5<0$
$ f(2)=6>0$
$ f(1)\, f(2)=-33<0$

% latex2html id marker 2526 $ \therefore$ There is a root for the given function in [1,2].
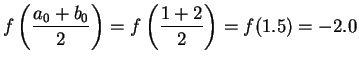
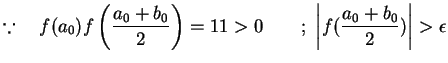
Set      $ a_{0}=1,\quad b_{0}=2,\quad \epsilon \approx10^{-6}$




Set
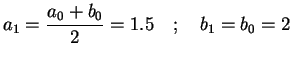
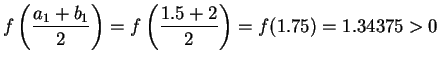
$ \displaystyle {f\left(\frac{a_{1}+b_{1}}{2}\right)= f\left(\frac{1.5+2}{2}\right)=f(1.75)=1.34375>0} $

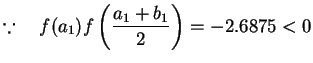$ \because\quad \displaystyle {f(a_{1})f\left(\frac{a_{1}+b_{1}}{2}\right)=-2.6875< 0 }$ and $ \vert f(1.75)\vert>\epsilon$

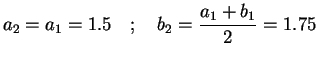
Set $ \displaystyle { a_{2}=a_{1}=1.5\quad ;\quad b_{2}=\frac{a_{1}+b_{1}}{2}=1.75 }$
Details of the remaining steps are provided in the table below:

 


    Bisection Method    
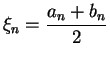Iteration no. $ a_n$ $ b_n$ $ \displaystyle {\xi_n=\frac{a_n+b_n}{2}}$ $ f(\xi_n)$
0 1.0000000000 2.0000000000 1.5000000000 -2.0000000000
1 1.5000000000 2.0000000000 1.7500000000 1.3437500000
2 1.5000000000 1.7500000000 1.6250000000 -0.4804687500
3 1.6250000000 1.7500000000 1.6875000000 0.3920898438
4 1.6250000000 1.6875000000 1.6562500000 -0.0538940430
5 1.6562500000 1.6875000000 1.6718750000 0.1666488647
6 1.6562500000 1.6718750000 1.6640625000 0.0557680130
7 1.6562500000 1.6640625000 1.6601562500 0.0007849932
8 1.6562500000 1.6601562500 1.6582031250 -0.0265924782
9 1.6582031250 1.6601562500 1.6591796875 -0.0129132364
10 1.6591796875 1.6601562500 1.6596679688 -0.0060664956
11 1.6596679688 1.6601562500 1.6599121094 -0.0026413449
12 1.6599121094 1.6601562500 1.6600341797 -0.0009283243
13 1.6600341797 1.6601562500 1.6600952148 -0.0000717027
14 1.6600952148 1.6601562500 1.6601257324 0.0003566360
15 1.6600952148 1.6601257324 1.6601104736 0.0001424643
16 1.6600952148 1.6601104736 1.6601028442 0.0000353802
17 1.6600952148 1.6601028442 1.6600990295 -0.0000181614
18 1.6600990295 1.6601028442 1.6601009369 0.0000086094

Example:
Solve $ 5 \sin^{2}x-8\cos^{5}x=0$ for the root in the interval $ [0.5,1.5]$ by Bisection method.

    Bisection Method    
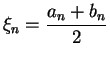Iteration no. $ a_n$ $ b_n$ $ \displaystyle {\xi_n=\frac{a_n+b_n}{2}}$ $ f(\xi_n)$
0 0.5000000000 1.5000000000 1.0000000000 3.1720056534
1 0.5000000000 1.0000000000 0.7500000000 0.6454265714
2 0.5000000000 0.7500000000 0.6250000000 -1.0943561792
3 0.6250000000 0.7500000000 0.6875000000 -0.1919542551
4 0.6875000000 0.7500000000 0.7187500000 0.2357951254
5 0.6875000000 0.7187500000 0.7031250000 0.0240836944
6 0.6875000000 0.7031250000 0.6953125000 -0.0834089667
7 0.6953125000 0.7031250000 0.6992187500 -0.0295295101
8 0.6992187500 0.7031250000 0.7011718750 -0.0026894973
9 0.7011718750 0.7031250000 0.7021484375 0.0107056862
10 0.7011718750 0.7021484375 0.7016601562 0.0040097744
11 0.7011718750 0.7016601562 0.7014160156 0.0006612621
12 0.7011718750 0.7014160156 0.7012939453 -0.0010144216
13 0.7012939453 0.7014160156 0.7013549805 -0.0001766436
14 0.7013549805 0.7014160156 0.7013854980 0.0002420362
15 0.7013549805 0.7013854980 0.7013702393 0.0000326998
16 0.7013549805 0.7013702393 0.7013626099 -0.0000715650
17 0.7013626099 0.7013702393 0.7013664246 -0.0000194324
18 0.7013664246 0.7013702393 0. 7013683 319 0.0000069206

Exercise: - Find the solutions of the following problems accurate to within using Bisection Method.

(1) for

(2) for

 


Next: False position or Regula: Up :Main Previous: Numerical Analysis